Graphing a Linear Inequality on the Number Line

---

---

Introduction

We represent inequalities by using a number line in this lesson.

• In the examples below, we show the range of true values for a given inequality.

• We use an open dot to represent < and > relationships; this symbol indicates that the point on the number line is not included within the range of possible values for the inequality.

• We use a closed dot to represent ≤ and ≥, when the two sides of the inequality could be equal.

Number Line

We recall that a number line is a horizontal line that has points, which correspond to numbers. The points are spaced according to the value of the number they correspond to; the points are equally spaced in a number line containing only whole numbers or integers.

Graph of the point 3

We graph numbers by representing them as points on the number line. For example, we graph "3" on the number line as shown below −

Graph of the Inequality x ≤ 3

We can also graph inequalities on the number line. The following graph represents the inequality x ≤ 3. The dark line represents all the numbers that satisfy x ≤ 3. If we pick any number on the dark line and plug it in for x, the inequality will be true.

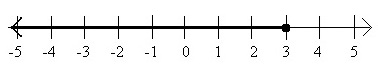
Graph of the Inequality x < 3

The following graph represents the inequality x < 3. Note that the open circle on 3 shows that 3 is not a solution to x < 3.

Graph of the Inequality x > 3

Here are the graphs of x > 3 and x ≥ 3, respectively

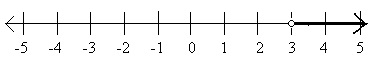
Graph of the Inequality x ≥ 3

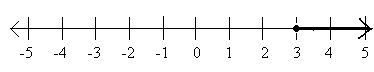
Graph of the Inequality x ≠ 3

An inequality with a ≠" sign has a solution set which is all the real numbers except a single point. Thus, to graph an inequality with a " ≠ " sign, graph the entire line with one point removed. For example, the graph of x ≠ 3 looks like −

Example 1

Graph the following inequality on the number line −

$\frac{x}{3}$ ≤ 7

Solution

Step 1:

$\frac{x}{3}$ ≤ 7; x ≤ $7 × 3$; x ≤ 21

We first locate the point 21 on the number line.

Step 2:

We put a closed circle on 21 and draw a thick line towards left to denote the inequality x ≤ 21

Example 2

Graph the following inequality on the number line −

x > 32

Solution

Step 1:

We first locate the point 32 on the number line.

Step 2:

We put a open circle on 32 and draw a thick line towards right to denote the inequality

x > 32