Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Search Tree and Hash Tables in compiler design?
Search Tree
A more effective technique to symbol table organization is to add two link fields, LEFT and RIGHT, to every record. We use these fields to link the records into a binary search tree.
This tree has the property that all names NAME (j) accessible from NAME (i) by following the link LEFT (i) and then following any sequence of links will precede NAME (i) in alphabetical order (symbolically, NAME (j) < NAME (i))
Similarly, all names NAME (k) accessible starting with RIGHT (i) will have the property that NAME (i) < NAME (k). Thus, if we are searching for NAME and have found the record for NAME (i) we need only follow LEFT (i) if NAME < NAME (i) and need only follow RIGHT (i) if NAME (i) < NAME ,of course, if NAME = NAME(i) we have found what we are looking for.
Binary Search Tree Algorithm
- Initially, Ptr will point to the root of the Tree.
- While Ptr ≠ NULL do
- If NAME = NAME (Ptr)
- then return true
- else if NAME<NAME (Ptr) then
- Ptr− LEFT(Ptr)
- else Ptr−= RIGHT (Ptr)
- End of Loop
Complexity
If names are encountered in random order, the average length of a path in the tree will be proportional to log n, where n is the number of names. Therefore each search follows one path from the root, the expected time needed to enter n names and make m inquiries is proportional to (n + m) log n, If n is greater than about 50, there is a clear advantage to the binary search tree over the linked list and probably over the linked self-organizing list.
Hash Tables
Hashing is an important procedure used to search the records of the symbol table. This method is superior to the list organization.
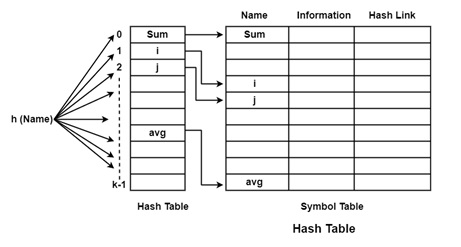
In the hashing scheme, two tables are maintained
- Hash Table
- Symbol Table
The hash table consists of K entries from 0 to K − 1. These entries are a pointer to the symbol table pointing to the names of the symbol table. It can decide whether "Name" is in the symbol table we use a hash function 'h' including h (Name) will result in an integer between 0 to K − 1. We can search any names by position = h(Name).
Using this position, we can access the exact locations of the name in the symbol table.
The hash function should result in the distribution of the name in the symbol table. The hash function should be that there will be a minimum number of collisions. Collision is a situation where the hash function results in the same location for storing names. There are various collision resolution techniques are open addressing, chaining, and rehashing.
Complexity
This scheme gives the capability of performing m access on n names in time proportional to n(n + m)/k for any constant k of our choice. Since k can be made as large as we like. This approach is usually superior to linear lists or search trees and is the technique of option for symbol tables in most situations, especially if storage is not incredibly costly.
2K+ Views
