Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Canonical Collection of LR (0) items in compiler design?
The LR (0) item for Grammar G consists of a production in which symbol dot (.) is inserted at some position in R.H.S of production.
For Example − For the production S → ABC, the generated LR (0) items will be −
S →∙ ABC
S → A ∙ BC
S → AB ∙ C
S → ABC ∙
Production S → ε generates only one item, i.e., S →∙
Canonical LR (0) collection helps to construct LR parser called Simple LR (SLR) parser.
To create Canonical LR (0) collection for Grammar, 3 things are required −
- Augmented Grammar
- Closure Function
- goto Function
Augmented Grammar − If grammar G has start symbol S, then augmented Grammar is new Grammar G′ with new start symbol S′. Also, it will contain the production S′ → S.
Closure − For a Context-Free Grammar G, if I is the set of items or states of grammar G, then −
Every item in I is in the closure (I).
If rule A → α. B β is a rule in closure (I) and there is another rule for B such as B → γ then closure (I) will consist of A → α. Bβ and B → . γ
Computation of Closure
procedure closure (I)
- begin
- Repeat
- for each rule A→α∙B β in I and B→γ in G
- 𝐀𝐝𝐝 B→∙γ in I
- Until no more elements can be added to I;
- end
- goto (𝐈,𝐗): If there is a production A→α∙X β in I then goto (I,X) is defined as closure of the set of items of A→α X∙β where I is set of items and X is grammar symbol (non-terminal).
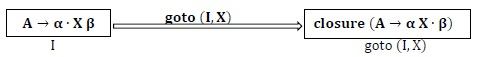
Algorithm for construction of Canonical collection of sets of LR (0) items
- begin
- C = {closure (S′ → ∙ S)}
- Repeat
- For each set of elements I in C and each grammar symbol X such that goto (I, X) is not empty and is not in C
- add goto (I, X) to C
- Until no more sets of elements can be added to C
- end
Example − Consider the Grammar
B → Ba | b
Find closure (I) and goto (I)
Solution
Let B →∙ Ba
Since B appears after the dot. Therefore other production with B on L.H.S with the dot on starting of R.H.S of production will be added to closure, i.e., B →∙ B is also added to closure (I).
∴ Closure(I) will be B → ∙ Ba (1)
B → ∙ b (2)
As, after the dot, we have B in (1)
∴ goto(I, B) will be B → B ∙ a
∵ After Dot, we have b in (2)
∴ goto(I, b) will be B → b ∙
4K+ Views
