Article Categories
- All Categories
-
 Data Structure
Data Structure
-
 Networking
Networking
-
 RDBMS
RDBMS
-
 Operating System
Operating System
-
 Java
Java
-
 MS Excel
MS Excel
-
 iOS
iOS
-
 HTML
HTML
-
 CSS
CSS
-
 Android
Android
-
 Python
Python
-
 C Programming
C Programming
-
 C++
C++
-
 C#
C#
-
 MongoDB
MongoDB
-
 MySQL
MySQL
-
 Javascript
Javascript
-
 PHP
PHP
What is two array representations in the symbol table?
Symbol Table is a data structure that supports an effective and efficient way of storing information about various names appearing in the source program. These names are used in the source code to identify the different program elements, like a variable, constants, procedures, and the labels of statements.
The symbol table is searched each time a name is encountered in the source text. When a new name or new data about an existing name is found, the content of the symbol table modifies.
Therefore, the symbol table must have an efficient mechanism for accessing the data held in the table also for adding new entries to the symbol table. In any case, the symbol table is a useful abstraction to aid the compiler to ascertain and verify the semantics, or meaning, of a piece of code. It will keep track of the names, types, locations, and properties of the symbols encountered in the program.
Two Array Representation of Symbol Table
In the symbol table, we may store different types of information and names. Information associated with other names also varies. Hence it is not advisory to allocate the same space to every kind of name appearing in the symbol table.
So, it can use two arrays to store names & information.
Character of Two Array Representation
- Instead of storing records in 1 array, we will be using 2 arrays.
- One array is used to store identifiers, and another array is used to store its attributes.
- Two arrays are connected with a rule.
If we suppose, an identifier takes 1 word of memory & Information corresponding to Identifiers or names takes 4 records. If we store identifier at position 2i and the corresponding information of identifier at 4i.
As information takes 4 words. Therefore, the information will be stored starting from 4i & ending at 4i + 3.
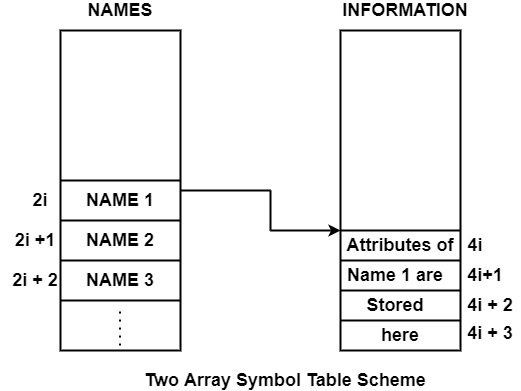
So, to Access the value of a particular Name & its corresponding information, we can just have to put the value of i.
Example− If we put i = 1
∴ Name at location 2i = 2 * 1 = 2 will be accessed.
Information at location = 4i = 4 will be accessed.
∴ Depending on various values of i, we can find different information corresponding to other names.
Advantages
- Faster Access to information.
- Low wastage of memory.
Disadvantage
- The requirement of Additional Array
- The complexity of the symbol table increases
- It can increase the necessity of memory.


