
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What are Precedence Functions in compiler design?
Precedence relations between any two operators or symbols in the precedence table can be converted to two precedence functions f & g that map terminals symbols to integers.
- If a <. b, then f (a) <. g (b)
- If a = b, then f (a) =. g (b)
- If a .> b, then f (a) .> g (b)
Here a, b represents terminal symbols. f (a) and g (b) represents the precedence functions that have an integer value.
Computations of Precedence Functions
- For each terminal a, create the symbol fa&ga.
- Make a node for each symbol.
If a =. b, then fa & gb are in same group or node.
If a =. b & c =. b, then fa & fc must be in same group or node.
- (a) If a <. b, Mark an edge from gb to fa.
(b) If a .>b, Mark an edge from fa to gb.
- If the graph constructed has a cycle, then no precedence functions exist.
- If there are no cycles.
(a) fa = Length of longest path beginning at the group of fa.
(b) ga = Length of the longest path from the group of ga.
Example1 − Construct precedence graph & precedence function for the following table.
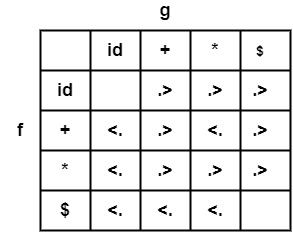
Solution
Step1 − Create Symbols![]()
Step2 − No symbol has equal precedence, as can be seen in the given table; therefore, each symbol will remain in a different node.
![]()
Step3 − If a <. b, create an edge from fa → ga
If a .>b, create an edge from gb → fa
Since, $ <. +,*, id. therefore, make an edge from g+, g*, gid to fs
Similarity + <. ,∗, id. ∴ make an edge from g*, gid to f+
Similarity * <. id. Therefore, Mark an edge from gid to f*.
Since, +,*, id . > $ therefore, Mark an edge from f+, f*, fid to gs.
Similarity +,*, id . > +. Mark an edge from f+, f*, fid to g+.
Similarity *, id . > *. Mark an edge from f*, fid to g.
Combining all the edges we get
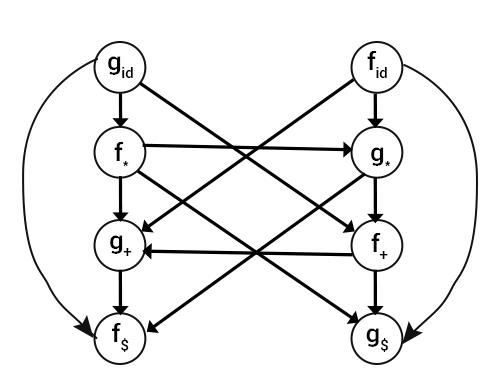
Step4 − Computing the maximum length of the path from each node, we get the following precedence functions
| Id | + | * | $ | |
| F | 4 | 2 | 4 | 0 |
| G | 5 | 1 | 3 | 0 |
Example2 − Construct precedence graph & precedence function for the following table.
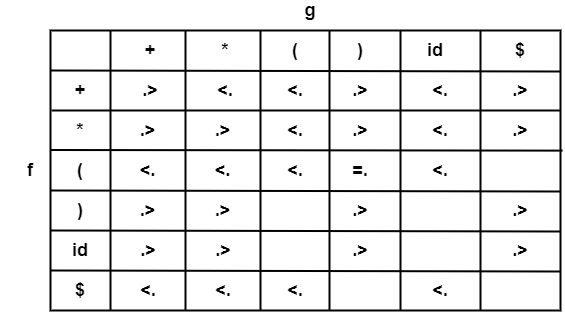
Solution
As we have (=.). Therefore f & g will be in the same group.
Computation of precedence graph
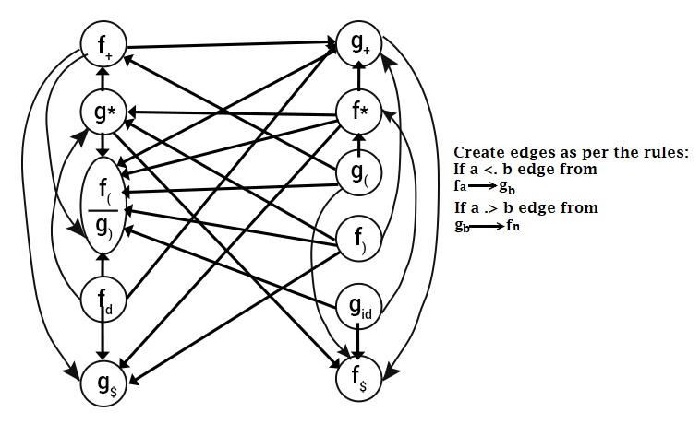
Computation of Precedence Function Table
Since f$ and g$ have no outgoing edges, f($ ) = g($ ) = 0.
Since f and g have no outgoing edges, f(( ) = g( )) = 0.
For all others, compute the path of the longest length starting from it.
For Example −
Take f+,
It has three outgoing edges and traces out its paths.
f+ → g$
f+ → f(
f+ → g+ → f( and f+ → g+ → f$
Select the path of maximum length, and the length is 2.
Hence, f+ = 2. computing all paths of f and g, we get Precedence table
| + | * | ( | ) | id | $ | |
| F | 2 | 4 | 0 | 4 | 4 | 0 |
| G | 1 | 3 | 5 | 0 | 5 | 0 |

