What are Derivations?

Derivations mean replacing a given string’s non-terminal by the right-hand side of the production rule. The sequence of applications of rules that makes the completed string of terminals from the starting symbol is known as derivation.

It can derive terminal strings, beginning with the start symbol, by repeatedly replacing a variable with some production. The language of CFG is a set of terminal symbols we can derive so. This language is called context Free Language.

Derivations are denoted by ⇒.

For example, consider a Grammar.

G=({S},{a,b},P,S), where, P contains following productions −

P={S→aSa |bSb | ∈}

In the above, S may be replaced by aSa or bSb or ∈.

Types of Derivations

There are two types of derivations which are as follows −

• Leftmost Derivation

A derivation A⇒*w is known as leftmost derivation if we use a production only to the leftmost variable at each step. Here, * means 0, 1, 2,………..n number of derivations.

• Rightmost Derivation

A derivation A⇒*w is the rightmost derivation if we use production to the rightmost variable at each step. It is also called Canonical Derivation.

Example1 − Let G be a CFG with productions.

S → AA
A → αB
B → b
B → ε

Find (1) Leftmost

• Rightmost derivation for string abab.

Solution

• Leftmost Derivation −

S ⇒^lm A $\underline{A}$

⇒^lm a $\underline{B}$ A

⇒^lm a b $\underline{A}$

⇒^lm a b a $\underline{B}$

⇒^lm a b a b

• Rightmost Derivation

S ⇒^rm A $\underline{A}$

⇒^rm A a $\underline{B}$

⇒^rm $\underline{A}$ a b

⇒^rm a $\underline{B}$ a b

⇒^rm a b a b

Example2 − Write a Context-Free Grammar for palindrome Language.

L={w c w^R| w ∈ {a,b}*} having middle symbol c. Here R means the reverse of a string.

Solution

Language represents a palindrome with a middle symbol 'c'.

∴ Grammar G=(V,∑,P,S) will have productions.

S → a S a
S → b S b
S → c

For example, To generate Palindrome a b c b a, the derivation is

S ⇒ a $\underline{S}$ a

⇒ a b $\underline{S}$ b a

⇒ a b c b a

Example3 − Write CFG for language which generates palindrome of binary numbers.

Solution

S → 0 S 0 | 1 S 1
S → 0 | 1 | ε

For example, To generate string 0 1 1 0, the derivation is

S ⇒ 0 S 0
⇒ 0 1 S 1 0
⇒ 0 1 ε 1 0
⇒ 0 1 1 0

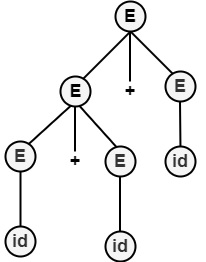
Example4 − Consider the Grammar given below −

E → E+E|E * E|id

Find

• Leftmost
• Rightmost Derivation for the string.

Solution

• Leftmost Derivation

E ⇒ $\underline{E}$+E

⇒ $\underline{E}$+E+E

⇒ id+E+E

⇒ id+id+E

⇒ id+id+id

• Rightmost Derivation

E ⇒ E+$\underline{E}$

⇒ E+E+$\underline{E}$

⇒ E+E+id

⇒ E+id+id

⇒ id+id+id