Using a net to find the surface area of a triangular prism

Introduction

In this lesson, we use nets of a triangular prism to find the surface area of the triangular prism.

The net of a solid figure is formed when a solid figure is unfolded along its edges and its faces are laid out in a pattern in two dimensions.

Nets of triangular prisms are made up of rectangles and triangles.

Using a net to find the surface area of a rectangular prism

Finding the areas of each of the rectangles and triangles of the net of a triangular prism and adding up those areas gives the surface area or total surface area of the triangular prism.

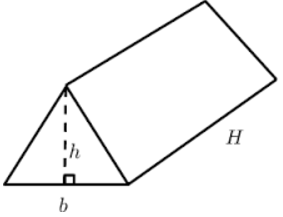
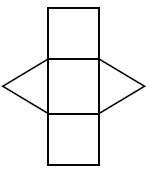
For example, let the legs of a right triangle that is base of a triangular prism are 3 and 4 units and height of the prism is 10 units. From the net, we can see that there are two congruent triangle faces and three rectangular faces whose areas are as follows. 6 square units and (3 + 4 + 5)10 = 120 square units. The surface area of prism then = 2(6) + 120 = 132 square units.

Surface Area of a Triangular Prism using Nets

Example 1:

Find the surface area of the following triangular prism using net.

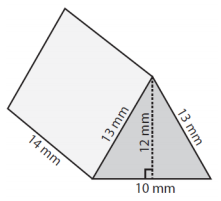
Solution

Step 1:

Using net the surface area of triangular prism

Sides of triangle base

a = 13mm; b = 13mm; c = 10mm; height h = 14mm

Triangle area = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$

= $\sqrt{18\left ( 18-13 \right )\left ( 18-13 \right )\left ( 18-10 \right )}$

= 60 square mm

Step 2:

Surface area of prism = 2 triangle area + h (a + b + c)

= 2(60) + (13 + 13 + 10)14

= 120 + 504

= 624 square cm

Example 2:

Find the surface area of the following triangular prism using net.

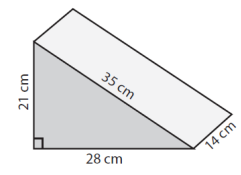
Solution

Step 1:

Using net the surface area of triangular prism

Sides of triangle base

a = 21cm; b = 28cm; c = 35cm; height h = 14cm

Triangle area = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$

= $\sqrt{42\left ( 42-21 \right )\left ( 42-28 \right )\left ( 42-35 \right )}$

= 294

Step 2:

Surface area of prism = 2 triangle area + h (a + b + c)

= 2(294) + (21 + 28 + 35)14

= 588 + 1176

= 1764 square cm