Surface area of a cube or a rectangular prism

In this lesson, we will learn how to calculate the surface area of a rectangular prism and solve problems on surface area of rectangular prisms.

A prism is a solid that has two parallel faces which are congruent polygons at both ends. These faces form the bases of the prism. A prism is named after the shape of its base. The other faces are in the shape of rectangles. They are called lateral faces.

The following diagram shows a rectangular prism.

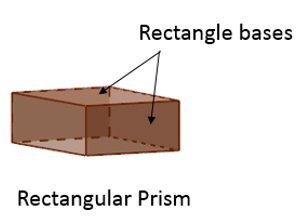
A right prism is a prism that has its bases perpendicular to its lateral surfaces.

The surface area of a prism is the total area of all its external faces.

To calculate the surface area of a rectangular prism

We calculate the area of each of the six faces of the prism.

We then add up all the areas to get the total surface area.

Formula to find the surface area of a prism

Surface area of prism = 2 × area of base + perimeter of base × height of prism

Formula to find the surface area of a rectangular prism

Surface area of a rectangular prism = 2 (l × w + w × h + l × h)

Where,

l – length of the prism

w – width of the prism and

h – height of the prism

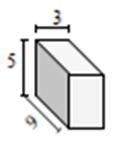
Find the surface area of the given rectangular prism in square cm.

Solution

Step 1:

Surface area of a rectangular prism = 2(l × w + w × h + 1 × h); l = 3 cm; w = 5 cm; h = 9 cm

Step 2:

Surface area of given prism = 2(3 × 5 + 3 × 9 + 9 × 5)

= 2(15 + 27 + 45)

= 174 square cm

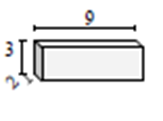
Find the surface area of the given rectangular prism in square cm.

Solution

Step 1:

Surface area of a rectangular prism = 2(l × w + w × h + l × h); l = 9 cm; w = 3 cm; h = 2 cm

Step 2:

Surface area of given prism = 2(9 × 3 + 9 × 2 + 3 × 2)

= 2(27 + 18 + 6)

= 102 square cm