
- Surface Areas
- Home
- Nets of solids
- Surface area of a cube or a rectangular prism
- Surface area of a rectangular prism made of unit cubes
- Distinguishing between surface area and volume
- Using a net to find the surface area of a rectangular prism
- Word problem involving the surface area of a rectangular prism
- Surface area of a triangular prism
- Using a net to find the surface area of a triangular prism
Surface area of a rectangular prism made of unit cubes
Introduction
In this lesson we consider rectangular prisms made of unit cubes. We find the surface area of the prism by counting the number of faces of the unit cubes that make up the prism.
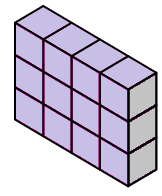
Surface area of the prism is the area of the paper that can be wrapped around the figure. Count the number of squares or unit squares on all six faces. Add all those squares to get the surface area of the prism.
Example 1
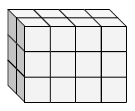
Find the length, width and height of the following rectangular prism. Then find its surface area.
Solution
Step 1:
Number of unit cubes along length, l = 4;
Number of unit cubes along width, w = 3;
Number of unit cube along height, h =2
Step 2:
The surface area = 2(l × w + w × h + l × h)
= 2(4 × 3 + 4 × 2 + 2 × 3)
= 2(12 + 8 + 6)
= 52 square units
Example 2
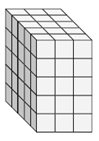
Find the length, width and height of the following rectangular prism. Then find its surface area.
Solution
Step 1:
Number of unit cubes along length, l = 3;
Number of unit cubes along width, w = 5;
Number of unit cube along height, h =5
Step 2:
The surface area = 2(l × w + w × h + l × h)
= 2(3 × 5 + 3 × 5 + 5 × 5)
= 2(15 + 15 + 25)
= 110 square units