
- Surface Areas
- Home
- Nets of solids
- Surface area of a cube or a rectangular prism
- Surface area of a rectangular prism made of unit cubes
- Distinguishing between surface area and volume
- Using a net to find the surface area of a rectangular prism
- Word problem involving the surface area of a rectangular prism
- Surface area of a triangular prism
- Using a net to find the surface area of a triangular prism
Surface area of a triangular prism
Introduction
In this lesson, we learn how to find the surface area of a triangular prism.
A triangular prism is a prism that has two congruent triangles as its bases connected by three rectangular lateral faces.
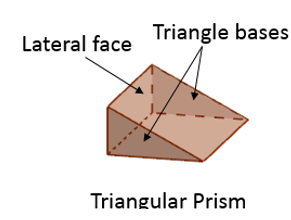
The surface area of the triangular prism is the sum total of the areas of its bases and its lateral faces.
Formula to find the surface area of a triangular prism
The Surface Area = 2 B + p h
where,
B is the area of the triangular base of prism
p perimeter of the base and
h the height of the prism
Example 1
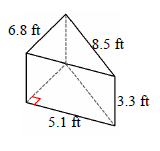
Find the surface area of the following triangular prism.
Solution
Step 1:
Area of triangle base A = 17.34 sq ft; height of prism h = 3.3 ft
Step 2:
Surface area of triangular prism = 2A + (a + b + c )h
= 2 × 17.34 + (6.8 + 8.5 + 5.1) × 3.3
= 102 square ft
Example 2
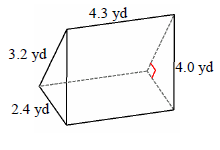
Find the surface area of the following triangular prism.
Solution
Step 1:
Area of triangle base A = 3.84 sq yd; height of prism h = 4.3 yd
Step 2:
Surface area of triangular prism = 2A + (a + b + c)h
= 2 × 3.84 + (2.4 + 3.2 + 4) × 4.3
= 48.96 square yd