Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Sum of the series 1, 3, 6, 10… (Triangular Numbers) in C++
In this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10 … (triangular number). Our task is to create a program to calculate the sum of the series.
Let’s brush up about triangular numbers before calculating the sum.
Triangular numbers are those numbers that can be represented in the form of a triangle.
A triangle is formed in such a way that the first row has one point, second has two, and so on.
Example
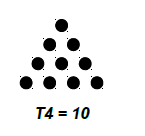
Let’s take an example to understand the problem,
Input
n = 4
Output
Explanation − sum = T1 + T2 + T3 + T4 = 1 + 3 + 6 + 10 = 20
A simple approach to solve this problem is to find all n triangle numbers. And adding them to the sum variable one by one.
Algorithm
Initialise sum = 0. Step 1: loop for i = 0 to n. And follow steps 2 and 3 Step 2: for each value of i, calculate the triangular numbers using the formula, t[i] = ∑ i = i*(i+1)/2. Step 3: Update sum value, sum += t[i]. Step 4: return sum.
Example
Program to illustrate the working of our solution,
#include <iostream>
using namespace std;
int calcSeriesSum(int n) {
int sum = 0;
for (int i=1; i<=n; i++)
sum += i*(i+1)/2;
return sum;
}
int main() {
int n = 6;
cout<<"Sum of the series 1, 3, 6, 10 ... (Triangular Numbers) is "<<calcSeriesSum(n);
return 0;
}Output
Sum of the series 1, 3, 6, 10 ... (Triangular Numbers) is 56
This is not the most effective solution as it takes O(n), time complexity.
A more effective solution is by using the direct formula for the sum.
If Ti is the i-th triangular number. Then,
T1 = 1
T2 = 3
T3 = 6
Tn = n*(n+1) /2
Sum of all triangular numbers is
sum = 1 + 3 + 6 + 10 + … sum = T1 + T2 + T3 + … + Tn sum = ∑ (Ti) , i -> 0 to n sum = ∑ (n)(n+1)/2 sum = ½ ∑ n2 + n sum = ½ ∑n^2 + ∑ n sum = ½ [ (n*(n+1)*(2n+1)/6) + (n*(n+1)/2) ] sum = ½ (n*(n+1)/2)*[ (2n+1)/3 + 1 ] sum = ¼ [n*(n+1)]*[(2n+1+3)/3] sum = ¼ [n*(n+1)]*[(2n+4)/3] sum = ¼ [n*(n+1)]*[2(n+2)/3] sum= â…™ [n*(n+1)*(n+2)]
This is the general formula for the sum of triangle numbers.
Example
Program to illustrate the working of our solution,
#include <iostream>
using namespace std;
int calcSeriesSum(int n) {
return ( ( n*(n + 1)*(n + 2) )/6);
}
int main() {
int n = 6;
cout<<"Sum of the series 1, 3, 6, 10 ... (Triangular Numbers) is "<<calcSeriesSum(n);
return 0;
}Output
Sum of the series 1, 3, 6, 10 ... (Triangular Numbers) is 56
1K+ Views
