
- Signals & Systems Home
- Signals & Systems Overview
- Introduction
- Signals Basic Types
- Signals Classification
- Signals Basic Operations
- Systems Classification
- Types of Signals
- Representation of a Discrete Time Signal
- Continuous-Time Vs Discrete-Time Sinusoidal Signal
- Even and Odd Signals
- Properties of Even and Odd Signals
- Periodic and Aperiodic Signals
- Unit Step Signal
- Unit Ramp Signal
- Unit Parabolic Signal
- Energy Spectral Density
- Unit Impulse Signal
- Power Spectral Density
- Properties of Discrete Time Unit Impulse Signal
- Real and Complex Exponential Signals
- Addition and Subtraction of Signals
- Amplitude Scaling of Signals
- Multiplication of Signals
- Time Scaling of Signals
- Time Shifting Operation on Signals
- Time Reversal Operation on Signals
- Even and Odd Components of a Signal
- Energy and Power Signals
- Power of an Energy Signal over Infinite Time
- Energy of a Power Signal over Infinite Time
- Causal, Non-Causal, and Anti-Causal Signals
- Rectangular, Triangular, Signum, Sinc, and Gaussian Functions
- Signals Analysis
- Types of Systems
- What is a Linear System?
- Time Variant and Time-Invariant Systems
- Linear and Non-Linear Systems
- Static and Dynamic System
- Causal and Non-Causal System
- Stable and Unstable System
- Invertible and Non-Invertible Systems
- Linear Time-Invariant Systems
- Transfer Function of LTI System
- Properties of LTI Systems
- Response of LTI System
- Fourier Series
- Fourier Series
- Fourier Series Representation of Periodic Signals
- Fourier Series Types
- Trigonometric Fourier Series Coefficients
- Exponential Fourier Series Coefficients
- Complex Exponential Fourier Series
- Relation between Trigonometric & Exponential Fourier Series
- Fourier Series Properties
- Properties of Continuous-Time Fourier Series
- Time Differentiation and Integration Properties of Continuous-Time Fourier Series
- Time Shifting, Time Reversal, and Time Scaling Properties of Continuous-Time Fourier Series
- Linearity and Conjugation Property of Continuous-Time Fourier Series
- Multiplication or Modulation Property of Continuous-Time Fourier Series
- Convolution Property of Continuous-Time Fourier Series
- Convolution Property of Fourier Transform
- Parseval’s Theorem in Continuous Time Fourier Series
- Average Power Calculations of Periodic Functions Using Fourier Series
- GIBBS Phenomenon for Fourier Series
- Fourier Cosine Series
- Trigonometric Fourier Series
- Derivation of Fourier Transform from Fourier Series
- Difference between Fourier Series and Fourier Transform
- Wave Symmetry
- Even Symmetry
- Odd Symmetry
- Half Wave Symmetry
- Quarter Wave Symmetry
- Fourier Transform
- Fourier Transforms
- Fourier Transforms Properties
- Fourier Transform – Representation and Condition for Existence
- Properties of Continuous-Time Fourier Transform
- Table of Fourier Transform Pairs
- Linearity and Frequency Shifting Property of Fourier Transform
- Modulation Property of Fourier Transform
- Time-Shifting Property of Fourier Transform
- Time-Reversal Property of Fourier Transform
- Time Scaling Property of Fourier Transform
- Time Differentiation Property of Fourier Transform
- Time Integration Property of Fourier Transform
- Frequency Derivative Property of Fourier Transform
- Parseval’s Theorem & Parseval’s Identity of Fourier Transform
- Fourier Transform of Complex and Real Functions
- Fourier Transform of a Gaussian Signal
- Fourier Transform of a Triangular Pulse
- Fourier Transform of Rectangular Function
- Fourier Transform of Signum Function
- Fourier Transform of Unit Impulse Function
- Fourier Transform of Unit Step Function
- Fourier Transform of Single-Sided Real Exponential Functions
- Fourier Transform of Two-Sided Real Exponential Functions
- Fourier Transform of the Sine and Cosine Functions
- Fourier Transform of Periodic Signals
- Conjugation and Autocorrelation Property of Fourier Transform
- Duality Property of Fourier Transform
- Analysis of LTI System with Fourier Transform
- Relation between Discrete-Time Fourier Transform and Z Transform
- Convolution and Correlation
- Convolution in Signals and Systems
- Convolution and Correlation
- Correlation in Signals and Systems
- System Bandwidth vs Signal Bandwidth
- Time Convolution Theorem
- Frequency Convolution Theorem
- Energy Spectral Density and Autocorrelation Function
- Autocorrelation Function of a Signal
- Cross Correlation Function and its Properties
- Detection of Periodic Signals in the Presence of Noise (by Autocorrelation)
- Detection of Periodic Signals in the Presence of Noise (by Cross-Correlation)
- Autocorrelation Function and its Properties
- PSD and Autocorrelation Function
- Sampling
- Signals Sampling Theorem
- Nyquist Rate and Nyquist Interval
- Signals Sampling Techniques
- Effects of Undersampling (Aliasing) and Anti Aliasing Filter
- Different Types of Sampling Techniques
- Laplace Transform
- Laplace Transforms
- Common Laplace Transform Pairs
- Laplace Transform of Unit Impulse Function and Unit Step Function
- Laplace Transform of Sine and Cosine Functions
- Laplace Transform of Real Exponential and Complex Exponential Functions
- Laplace Transform of Ramp Function and Parabolic Function
- Laplace Transform of Damped Sine and Cosine Functions
- Laplace Transform of Damped Hyperbolic Sine and Cosine Functions
- Laplace Transform of Periodic Functions
- Laplace Transform of Rectifier Function
- Laplace Transforms Properties
- Linearity Property of Laplace Transform
- Time Shifting Property of Laplace Transform
- Time Scaling and Frequency Shifting Properties of Laplace Transform
- Time Differentiation Property of Laplace Transform
- Time Integration Property of Laplace Transform
- Time Convolution and Multiplication Properties of Laplace Transform
- Initial Value Theorem of Laplace Transform
- Final Value Theorem of Laplace Transform
- Parseval's Theorem for Laplace Transform
- Laplace Transform and Region of Convergence for right sided and left sided signals
- Laplace Transform and Region of Convergence of Two Sided and Finite Duration Signals
- Circuit Analysis with Laplace Transform
- Step Response and Impulse Response of Series RL Circuit using Laplace Transform
- Step Response and Impulse Response of Series RC Circuit using Laplace Transform
- Step Response of Series RLC Circuit using Laplace Transform
- Solving Differential Equations with Laplace Transform
- Difference between Laplace Transform and Fourier Transform
- Difference between Z Transform and Laplace Transform
- Relation between Laplace Transform and Z-Transform
- Relation between Laplace Transform and Fourier Transform
- Laplace Transform – Time Reversal, Conjugation, and Conjugate Symmetry Properties
- Laplace Transform – Differentiation in s Domain
- Laplace Transform – Conditions for Existence, Region of Convergence, Merits & Demerits
- Z Transform
- Z-Transforms (ZT)
- Common Z-Transform Pairs
- Z-Transform of Unit Impulse, Unit Step, and Unit Ramp Functions
- Z-Transform of Sine and Cosine Signals
- Z-Transform of Exponential Functions
- Z-Transforms Properties
- Properties of ROC of the Z-Transform
- Z-Transform and ROC of Finite Duration Sequences
- Conjugation and Accumulation Properties of Z-Transform
- Time Shifting Property of Z Transform
- Time Reversal Property of Z Transform
- Time Expansion Property of Z Transform
- Differentiation in z Domain Property of Z Transform
- Initial Value Theorem of Z-Transform
- Final Value Theorem of Z Transform
- Solution of Difference Equations Using Z Transform
- Long Division Method to Find Inverse Z Transform
- Partial Fraction Expansion Method for Inverse Z-Transform
- What is Inverse Z Transform?
- Inverse Z-Transform by Convolution Method
- Transform Analysis of LTI Systems using Z-Transform
- Convolution Property of Z Transform
- Correlation Property of Z Transform
- Multiplication by Exponential Sequence Property of Z Transform
- Multiplication Property of Z Transform
- Residue Method to Calculate Inverse Z Transform
- System Realization
- Cascade Form Realization of Continuous-Time Systems
- Direct Form-I Realization of Continuous-Time Systems
- Direct Form-II Realization of Continuous-Time Systems
- Parallel Form Realization of Continuous-Time Systems
- Causality and Paley Wiener Criterion for Physical Realization
- Discrete Fourier Transform
- Discrete-Time Fourier Transform
- Properties of Discrete Time Fourier Transform
- Linearity, Periodicity, and Symmetry Properties of Discrete-Time Fourier Transform
- Time Shifting and Frequency Shifting Properties of Discrete Time Fourier Transform
- Inverse Discrete-Time Fourier Transform
- Time Convolution and Frequency Convolution Properties of Discrete-Time Fourier Transform
- Differentiation in Frequency Domain Property of Discrete Time Fourier Transform
- Parseval’s Power Theorem
- Miscellaneous Concepts
- What is Mean Square Error?
- What is Fourier Spectrum?
- Region of Convergence
- Hilbert Transform
- Properties of Hilbert Transform
- Symmetric Impulse Response of Linear-Phase System
- Filter Characteristics of Linear Systems
- Characteristics of an Ideal Filter (LPF, HPF, BPF, and BRF)
- Zero Order Hold and its Transfer Function
- What is Ideal Reconstruction Filter?
- What is the Frequency Response of Discrete Time Systems?
- Basic Elements to Construct the Block Diagram of Continuous Time Systems
- BIBO Stability Criterion
- BIBO Stability of Discrete-Time Systems
- Distortion Less Transmission
- Distortionless Transmission through a System
- Rayleigh’s Energy Theorem
Convolution and Correlation
Convolution
Convolution is a mathematical operation used to express the relation between input and output of an LTI system. It relates input, output and impulse response of an LTI system as
$$ y (t) = x(t) * h(t) $$
Where y (t) = output of LTI
x (t) = input of LTI
h (t) = impulse response of LTI
There are two types of convolutions:
Continuous convolution
Discrete convolution
Continuous Convolution

$ y(t) \,\,= x (t) * h (t) $
$= \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$
(or)
$= \int_{-\infty}^{\infty} x(t - \tau) h (\tau)d\tau $
Discrete Convolution

$y(n)\,\,= x (n) * h (n)$
$= \Sigma_{k = - \infty}^{\infty} x(k) h (n-k) $
(or)
$= \Sigma_{k = - \infty}^{\infty} x(n-k) h (k) $
By using convolution we can find zero state response of the system.
Deconvolution
Deconvolution is reverse process to convolution widely used in signal and image processing.
Properties of Convolution
Commutative Property
$ x_1 (t) * x_2 (t) = x_2 (t) * x_1 (t) $
Distributive Property
$ x_1 (t) * [x_2 (t) + x_3 (t) ] = [x_1 (t) * x_2 (t)] + [x_1 (t) * x_3 (t)]$
Associative Property
$x_1 (t) * [x_2 (t) * x_3 (t) ] = [x_1 (t) * x_2 (t)] * x_3 (t) $
Shifting Property
$ x_1 (t) * x_2 (t) = y (t) $
$ x_1 (t) * x_2 (t-t_0) = y (t-t_0) $
$ x_1 (t-t_0) * x_2 (t) = y (t-t_0) $
$ x_1 (t-t_0) * x_2 (t-t_1) = y (t-t_0-t_1) $
Convolution with Impulse
$ x_1 (t) * \delta (t) = x(t) $
$ x_1 (t) * \delta (t- t_0) = x(t-t_0) $
Convolution of Unit Steps
$ u (t) * u (t) = r(t) $
$ u (t-T_1) * u (t-T_2) = r(t-T_1-T_2) $
$ u (n) * u (n) = [n+1] u(n) $
Scaling Property
If $x (t) * h (t) = y (t) $
then $x (a t) * h (a t) = {1 \over |a|} y (a t)$
Differentiation of Output
if $y (t) = x (t) * h (t)$
then $ {dy (t) \over dt} = {dx(t) \over dt} * h (t) $
or
$ {dy (t) \over dt} = x (t) * {dh(t) \over dt}$
Note:
Convolution of two causal sequences is causal.
Convolution of two anti causal sequences is anti causal.
Convolution of two unequal length rectangles results a trapezium.
Convolution of two equal length rectangles results a triangle.
A function convoluted itself is equal to integration of that function.
Example: You know that $u(t) * u(t) = r(t)$
According to above note, $u(t) * u(t) = \int u(t)dt = \int 1dt = t = r(t)$
Here, you get the result just by integrating $u(t)$.
Limits of Convoluted Signal
If two signals are convoluted then the resulting convoluted signal has following range:
Sum of lower limits < t < sum of upper limits
Ex: find the range of convolution of signals given below

Here, we have two rectangles of unequal length to convolute, which results a trapezium.
The range of convoluted signal is:
Sum of lower limits < t < sum of upper limits
$-1+-2 < t < 2+2 $
$-3 < t < 4 $
Hence the result is trapezium with period 7.
Area of Convoluted Signal
The area under convoluted signal is given by $A_y = A_x A_h$
Where Ax = area under input signal
Ah = area under impulse response
Ay = area under output signal
Proof: $y(t) = \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$
Take integration on both sides
$ \int y(t)dt \,\,\, =\int \int_{-\infty}^{\infty}\, x (\tau) h (t-\tau)d\tau dt $
$ =\int x (\tau) d\tau \int_{-\infty}^{\infty}\, h (t-\tau) dt $
We know that area of any signal is the integration of that signal itself.
$\therefore A_y = A_x\,A_h$
DC Component
DC component of any signal is given by
$\text{DC component}={\text{area of the signal} \over \text{period of the signal}}$
Ex: what is the dc component of the resultant convoluted signal given below?

Here area of x1(t) = length breadth = 1 3 = 3
area of x2(t) = length breadth = 1 4 = 4
area of convoluted signal = area of x1(t) area of x2(t)
= 3 4 = 12
Duration of the convoluted signal = sum of lower limits < t < sum of upper limits
= -1 + -2 < t < 2+2
= -3 < t < 4
Period=7
$\therefore$ Dc component of the convoluted signal = $\text{area of the signal} \over \text{period of the signal}$
Dc component = ${12 \over 7}$
Discrete Convolution
Let us see how to calculate discrete convolution:
i. To calculate discrete linear convolution:
Convolute two sequences x[n] = {a,b,c} & h[n] = [e,f,g]

Convoluted output = [ ea, eb+fa, ec+fb+ga, fc+gb, gc]
Note: if any two sequences have m, n number of samples respectively, then the resulting convoluted sequence will have [m+n-1] samples.
Example: Convolute two sequences x[n] = {1,2,3} & h[n] = {-1,2,2}

Convoluted output y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]
= [-1, 0, 3, 10, 6]
Here x[n] contains 3 samples and h[n] is also having 3 samples so the resulting sequence having 3+3-1 = 5 samples.
ii. To calculate periodic or circular convolution:
Periodic convolution is valid for discrete Fourier transform. To calculate periodic convolution all the samples must be real. Periodic or circular convolution is also called as fast convolution.
If two sequences of length m, n respectively are convoluted using circular convolution then resulting sequence having max [m,n] samples.
Ex: convolute two sequences x[n] = {1,2,3} & h[n] = {-1,2,2} using circular convolution

Normal Convoluted output y[n] = [ -1, -2+2, -3+4+2, 6+4, 6].
= [-1, 0, 3, 10, 6]
Here x[n] contains 3 samples and h[n] also has 3 samples. Hence the resulting sequence obtained by circular convolution must have max[3,3]= 3 samples.
Now to get periodic convolution result, 1st 3 samples [as the period is 3] of normal convolution is same next two samples are added to 1st samples as shown below:
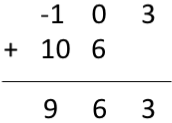
$\therefore$ Circular convolution result $y[n] = [9\quad 6\quad 3 ]$
Correlation
Correlation is a measure of similarity between two signals. The general formula for correlation is
$$ \int_{-\infty}^{\infty} x_1 (t)x_2 (t-\tau) dt $$
There are two types of correlation:
Auto correlation
Cros correlation
Auto Correlation Function
It is defined as correlation of a signal with itself. Auto correlation function is a measure of similarity between a signal & its time delayed version. It is represented with R($\tau$).
Consider a signals x(t). The auto correlation function of x(t) with its time delayed version is given by
$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x(t-\tau) dt \quad \quad \text{[+ve shift]} $$
$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t)x(t + \tau) dt \quad \quad \text{[-ve shift]} $$
Where $\tau$ = searching or scanning or delay parameter.
If the signal is complex then auto correlation function is given by
$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x * (t-\tau) dt \quad \quad \text{[+ve shift]} $$
$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t + \tau)x * (t) dt \quad \quad \text{[-ve shift]} $$
Properties of Auto-correlation Function of Energy Signal
Auto correlation exhibits conjugate symmetry i.e. R ($\tau$) = R*(-$\tau$)
-
Auto correlation function of energy signal at origin i.e. at $\tau$=0 is equal to total energy of that signal, which is given as:
R (0) = E = $ \int_{-\infty}^{\infty}\,|\,x(t)\,|^2\,dt $
Auto correlation function $\infty {1 \over \tau} $,
Auto correlation function is maximum at $\tau$=0 i.e |R ($\tau$) | ≤ R (0) ∀ $\tau$
-
Auto correlation function and energy spectral densities are Fourier transform pairs. i.e.
$F.T\,[ R (\tau) ] = \Psi(\omega)$
$\Psi(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d \tau$
$ R (\tau) = x (\tau)* x(-\tau) $
Auto Correlation Function of Power Signals
The auto correlation function of periodic power signal with period T is given by
$$ R (\tau) = \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x* (t-\tau) dt $$
Properties
Auto correlation of power signal exhibits conjugate symmetry i.e. $ R (\tau) = R*(-\tau)$
-
Auto correlation function of power signal at $\tau = 0$ (at origin)is equal to total power of that signal. i.e.
$R (0)= \rho $
Auto correlation function of power signal $\infty {1 \over \tau}$,
-
Auto correlation function of power signal is maximum at $\tau$ = 0 i.e.,
$ | R (\tau) | \leq R (0)\, \forall \,\tau$
-
Auto correlation function and power spectral densities are Fourier transform pairs. i.e.,
$F.T[ R (\tau) ] = s(\omega)$
$s(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d\tau$
$R (\tau) = x (\tau)* x(-\tau) $
Density Spectrum
Let us see density spectrums:
Energy Density Spectrum
Energy density spectrum can be calculated using the formula:
$$ E = \int_{-\infty}^{\infty} |\,x(f)\,|^2 df $$
Power Density Spectrum
Power density spectrum can be calculated by using the formula:
$$P = \Sigma_{n = -\infty}^{\infty}\, |\,C_n |^2 $$
Cross Correlation Function
Cross correlation is the measure of similarity between two different signals.
Consider two signals x1(t) and x2(t). The cross correlation of these two signals $R_{12}(\tau)$ is given by
$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2 (t-\tau)\, dt \quad \quad \text{[+ve shift]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2 (t)\, dt \quad \quad \text{[-ve shift]}$$
If signals are complex then
$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2^{*}(t-\tau)\, dt \quad \quad \text{[+ve shift]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2^{*} (t)\, dt \quad \quad \text{[-ve shift]}$$
$$R_{21} (\tau) = \int_{-\infty}^{\infty} x_2 (t)x_1^{*}(t-\tau)\, dt \quad \quad \text{[+ve shift]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_2 (t+\tau)x_1^{*} (t)\, dt \quad \quad \text{[-ve shift]}$$
Properties of Cross Correlation Function of Energy and Power Signals
Auto correlation exhibits conjugate symmetry i.e. $R_{12} (\tau) = R^*_{21} (-\tau)$.
-
Cross correlation is not commutative like convolution i.e.
$$ R_{12} (\tau) \neq R_{21} (-\tau) $$
-
If R12(0) = 0 means, if $ \int_{-\infty}^{\infty} x_1 (t) x_2^* (t) dt = 0$, then the two signals are said to be orthogonal.
For power signal if $ \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x^* (t)\,dt $ then two signals are said to be orthogonal.
-
Cross correlation function corresponds to the multiplication of spectrums of one signal to the complex conjugate of spectrum of another signal. i.e.
$$ R_{12} (\tau) \leftarrow \rightarrow X_1(\omega) X_2^*(\omega)$$
This also called as correlation theorem.
Parseval's Theorem
Parseval's theorem for energy signals states that the total energy in a signal can be obtained by the spectrum of the signal as
$ E = {1\over 2 \pi} \int_{-\infty}^{\infty} |X(\omega)|^2 d\omega $
Note: If a signal has energy E then time scaled version of that signal x(at) has energy E/a.