Sec 60

Introduction

The link between a right triangle's side ratio and angle is the subject of the mathematical branch of trigonometry. The ratio used to study this relationship is called the trigonometric ratio. That is, sine, cosine, tangent, cotangent, second, cotangent. The hypotenuse, the base (which is adjacent), and the perpendicular are the three sides of a right-angled triangle from which trigonometric ratios in geometry are obtained.

The name "trigonometry" is made up of the phrases "Trigonon" and "Metron," which denote a triangle and a measure, respectively. The ratio of the hypotenuse's length to the neighbouring side's (base) length is known as the sec of an angle in a right triangle. In this tutorial, we will discuss the value of sec60 degrees and trigonometry.

Trigonometric Functions

The primary divisions of trigonometric functions are tangent, sine, and cosine angles. Additionally, the main functions can be used to generate the three cotangent functions, second, and cotangent. In contrast to the primary trigonometric functions, the other three functions are generally utilized more frequently. For a description of these three key qualities, see the accompanying image. Trigonometry is usually defined as a right triangle.

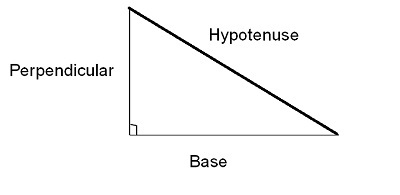
Sine function

The ratio of the hypotenuse's length to the opposite side's length (Perpendicular) is known as the angle sine function. The values of sin from the triangle above are

$$\mathrm{\sin\theta\:=\:\frac{Perpendicular}{Hypotenuse}}$$

Cos function

It is the ratio of the hypotenuse's length to the length of the neighbouring side (Base). The cos function is derived as follows from the triangle mentioned above

$$\mathrm{\cos\theta\:=\:\frac{Base}{Hypotenuse}}$$

Tan function

The ratio of the lengths on the adjacent and opposite sides is known as the tangent function.

$$\mathrm{\tan\theta\:=\:\frac{Perpendicular}{Base}}$$

Three further functions that are derived from the sine, cosine, and tangent fundamental functions are the secant, cosecant, and cotangent.

$$\mathrm{\cot\theta\:=\:\frac{1}{\tan\theta}\:=\:\frac{Base}{Perpendicular}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$$

Trigonometric equations or identities are the equations that apply to right triangles. Here are some of the special trigonometric formulas −

Pythagoras identity

$$\mathrm{\sin^{2}\:\theta\:+\:\cos^{2}\:\theta\:=\:1}$$

$$\mathrm{\tan^{2}\:\theta\:+\:1\:=\:\sec^{2}\:\theta}$$

$$\mathrm{\cot^{2}\:\theta\:+\:1\:=\:cosec^{2}\:\theta}$$

$$\mathrm{\sin\:2\theta\:=\:2\sin\:\theta\:\cos\:\theta}$$

$$\mathrm{\cos\:2\theta\:=\:\cos^{2}\theta\:-\:\sin^{2}\:\theta}$$

$$\mathrm{\cos\:2\theta\:=\:\frac{2\:\tan\:\theta}{1\:-\:\tan^{2}\:\theta}}$$

$$\mathrm{\cos\:2\theta\:=\:\frac{\cot^{2}\:\theta\:-\:1}{2\:\cot\:\theta}}$$

Difference and sum identities

Angles u and v have the following relationship −

$$\mathrm{\sin(u\:+\:v)\:=\:\sin(u)\:\cos(v)\:+\:cos(u)\sin(v)}$$

$$\mathrm{\cos(u\:+\:v)\:=\:\cos(u)\:\cos(v)\:-\:sin(u)\sin(v)}$$

$$\mathrm{\sin(u\:-\:v)\:=\:\sin(u)\:\cos(v)\:-\:cos(u)\sin(v)}$$

$$\mathrm{\cos(u\:-\:v)\:=\:\cos(u)\:\cos(v)\:+\:sin(u)\sin(v)}$$

$$\mathrm{\tan(u\:+\:v)\:=\:\frac{\tan(u)\:-\:\tan(v)}{1\:+\:\tan(u)\:\tan(v)}}$$

$$\mathrm{\tan(u\:-\:v)\:=\:\frac{\tan(u)\:-\:\tan(v)}{1\:+\:\tan(u)\:\tan(v)}}$$

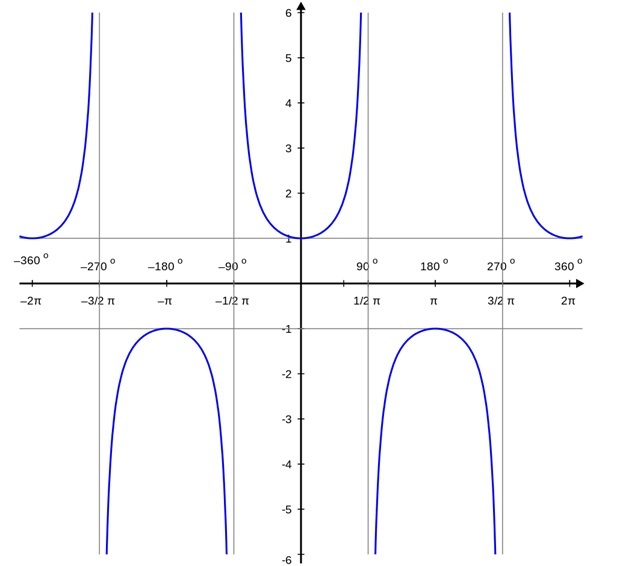
Secant Function and its Graph

In trigonometry, the secant function is periodic. The ratio of the hypotenuse's length to the base's length in a right-angled triangle is known as the secant function or sec function. It is also written as $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$

since it is the reciprocal of the cosine function. Since we are already familiar with the cosine graph, graphing secant becomes extremely simple. By determining the reciprocal of each cosine value, we can quickly create the graph for sec x. When cos x has a very small value, sec x will have a very large value. Specifically, determining $\mathrm{\frac{1}{y}}$ for each value of y along the line $\mathrm{y\:=\:cosx}$. The following table displays some angles in radians

x	$\mathrm{\cos\:x}$	$\mathrm{\sec\:x}$
0	1	1
$\mathrm{\frac{\pi}{6}}$	$\mathrm{\frac{\sqrt{3}}{2}}$	$\mathrm{\frac{2}{\sqrt{3}}}$
$\mathrm{\frac{\pi}{4}}$	$\mathrm{\frac{1}{\sqrt{2}}}$	$\mathrm{\sqrt{2}}$
$\mathrm{\frac{\pi}{3}}$	$\mathrm{\frac{1}{2}}$	2
$\mathrm{\frac{\pi}{2}}$	0	Not defined

Additionally, we notice that the secant function goes to infinity when the cosine function's value is zero, meaning the secant is undefined at that point. As a result, we get the sec x graph as follows −

Sec 60

Sec 60 degrees is worth 2, so. Sec 60 degrees is represented by $$in radians. The angle 60° for sec 60 degrees is located between 0° and 90° (First Quadrant). Sec 60° value = 2 because secant function is positive in the first quadrant.

Given that the secant function is a periodic function, sec 60° can be represented as $$

Note − Secant is an even function, $\mathrm{\sec(-60°)\:equals\:\sec(60°)}$

Significance of Secant Function

One of the important trigonometric functions in trigonometry is the secant function. A straight line or ray that touches a curve, particularly a circle, more than once then it is equivalent to the right-angled triangle's hypotenuse to base ratio. The reciprocal of the cosine function is another name for the secant function

Solved Examples

Example 1 − Find the value of the 𝑡𝑎𝑛 𝜃 when the value of $\mathrm{\sec\:\theta}$ is 2.

Solution − We know that the relation between $\mathrm{\tan\:\theta}$ and $\mathrm{\sec\:\theta}$ is

$$\mathrm{\sec^{2}\:\theta\:=\:1\:+\:tan^{2}\:\theta}$$

$$\mathrm{\tan^{2}\:\theta\:=\:\sec^{2}\:\theta\:-\:1}$$

It is given that the value of $\mathrm{\sec\:\theta}$ is 2, now put this value in the above equation,

$$\mathrm{\tan^{2}\:\theta\:=\:2^{2}\:-\:1}$$

$$\mathrm{\tan^{2}\:\theta\:=\:4\:-\:1}$$

$$\mathrm{\tan^{2}\:\theta\:=\:3}$$

$$\mathrm{\tan\:\theta\:=\:\sqrt{3}}$$

Example 2 − Find the value of 𝑡𝑎𝑛𝜃 when the value of 𝑠𝑒𝑐𝜃 is 1.

Solution − It is given than $\mathrm{\sec\:\theta\:=\:1}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\theta\:=\:0°}$

so, $\mathrm{\tan\:\theta\:=\:\tan0°\:=\:0}$

Example 3 − Find the value of 𝑐𝑜𝑠 𝜃 when the value of 𝑠𝑒𝑐𝜃 is 1.

Solution − We know that $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\cos\:\theta\:=\:\frac{1}{\sec\:\theta}}$

$\mathrm{\:\:Significance of Secant Function\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\cos\:\theta\:=\:\frac{1}{1}\:=\:1}$

Example 4 − What is the domain of secant function?

Solution − The domain of the secant function is $\mathrm{R\:-\:(2n\:+\:1)\:\frac{\pi}{2}}$ where R is real numbers.

Example 5 − Find the relation between $\mathrm{\cos\:2\theta\:and\:\sec\:\theta}$

Solution − We know that the $\mathrm{\cos\:2\theta\:=\:cos^{2}\:\theta\:-\:\sin^{2}\:\theta}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sin^{2}\:\theta\:+\:\cos^{2}\:\theta\:=\:1}$

$\mathrm{\Rightarrow\:\sin^{2}\:\theta\:=\:1\:-\:\cos^{2}\:\theta}$

Now put this value in the above equation

$\mathrm{\cos\:2\theta\:=\:cos^{2}\:\theta\:-\:(1\:-\:\cos^{2}\:\theta)}$

$\mathrm{\cos\:2\theta\:=\:2\cos^{2}\:\theta\:-\:1}$

we know that $\mathrm{\sec\:\theta\:=\frac{1}{\cos\:\theta}}$ put this value in above equation

$\mathrm{\cos\:2\theta\:=\:\frac{2}{\sec^{2}\:\theta}\:-\:1}$

Example 6 − Find the value of $\mathrm{2\tan\:45°\:+\:\sec\:60°}$

Solution − $\mathrm{2\tan\:45°\:+\:\sec\:60°}$

Now put their values $\mathrm{2\tan\:45°\:+\:\sec\:60°\:=\:2\:+\:2}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:4}$

Example 7 − Simplify $\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}}$

Solution − Given equation is $\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}}$

we know that the value of $\mathrm{\tan\:45°}$ is 1 and the value of 𝑠𝑒𝑐60° is 2

So, $\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}\:=\:\frac{4\:+\:1}{2}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{5}{2}}$

Example 8 − Simplify $\mathrm{\sec60°\:-\:\cos60°}$

Solution − Given equation is $\mathrm{\sec60°\:-\:\cos60°}$

$\mathrm{\Rightarrow\:2\:-\:\frac{1}{2}}$

$\mathrm{\Rightarrow\:\frac{3}{2}}$

Example 9 − Simplify $\mathrm{\frac{\sec60°}{\cos60°}\:-\:\frac{\cos60°}{\sec60°}}$

Solution − Given equation is $\mathrm{\frac{\sec60°}{\cos60°}\:-\:\frac{\cos60°}{\sec60°}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\frac{2}{\frac{1}{2}}\:-\:\frac{\frac{1}{2}}{2}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:4\:-\:\frac{1}{4}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\frac{15}{4}}$

Conclusion

The value of the secant trigonometric function for an angle of 0 degrees (Sec 60 degrees) is two. The ratio of the hypotenuse's length to the base's length in a right-angled triangle is known as the secant function or sec function. It is also written as $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$since it is the reciprocal of the cosine function

FAQs

1. What do you mean by secant function?

The ratio of the hypotenuse's length to the base's length in a right-angled triangle is known as the secant function or sec function

2. What do you mean by Trigonometry?

The link between a right triangle's side ratio and angle is the subject of the mathematical branch of trigonometry.

3. What is the value of the sec function at 60 degrees?

The value of the secant trigonometric function for an angle of 60 degrees (Sec 60 degrees) is 2 .

4. Find the nature (odd, even) of the secant function?

The secant function is an even function because $\mathrm{\sec(-x)\:=\:\sec\:x}$ for all x.

5. What is the relation between cos and sec function?

Sec function is also written as $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$ because it is the reciprocal of the cosine function.