Sec 0

Introduction

The notion of trigonometry was developed by the Greek mathematician Hipparchus, while the name trigonometry is a 16th-century Latin derivative.

Trigonometry is one of the most important branches of mathematics. The name "trigonometry" is made up of the phrases "Trigonon" and "Metron," which denote a triangle and a measure, respectively. It is the study of the relationship between the sides and angles of a right-angled triangle. The ratio of the hypotenuse's length to the neighbouring side's (base) length is known as the sec of an angle in a right triangle. The angle 0° for sec 0 degrees is located on the positive x-axis. Therefore, sec 0° value = 1.

In this tutorial, we will discuss the value of sec0 and trigonometry.

Trigonometric Functions

The link between a right triangle's side ratio and angle is the subject of the mathematical branch of trigonometry. The ratio used to study this relationship is called the trigonometric ratio. The primary divisions of trigonometric functions are tangent, sine, and cosine angles. The main functions can also generate the three cotangents, second, and cotangent functions.

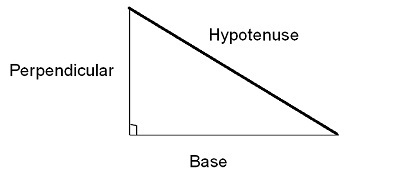
Sine function

The ratio of the hypotenuse's length to the opposite side's length (Perpendicular) is known as the angle sine function. The values of sin from the triangle above are

$$\mathrm{\sin\theta\:=\:\frac{Perpendicular}{Hypotenuse}}$$

Cos function

It is the ratio of the hypotenuse's length to the length of the neighbouring side (Base). The cos function is derived as follows from the triangle mentioned above

$$\mathrm{\cos\theta\:=\:\frac{Base}{Hypotenuse}}$$

Tan function

The ratio of the lengths on the adjacent and opposite sides is known as the tangent function.

$$\mathrm{\tan\theta\:=\:\frac{Perpendicular}{Base}}$$

Three further functions that are derived from the sine, cosine, and tangent fundamental functions are the secant, cosecant, and cotangent.

$$\mathrm{\cot\theta\:=\:\frac{1}{\tan\theta}\:=\:\frac{Base}{Perpendicular}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$$

$$\mathrm{\:cosec\theta\:=\:\frac{1}{\sin\theta}\:=\:\frac{Hypotenuse}{Perpendicular}}$$

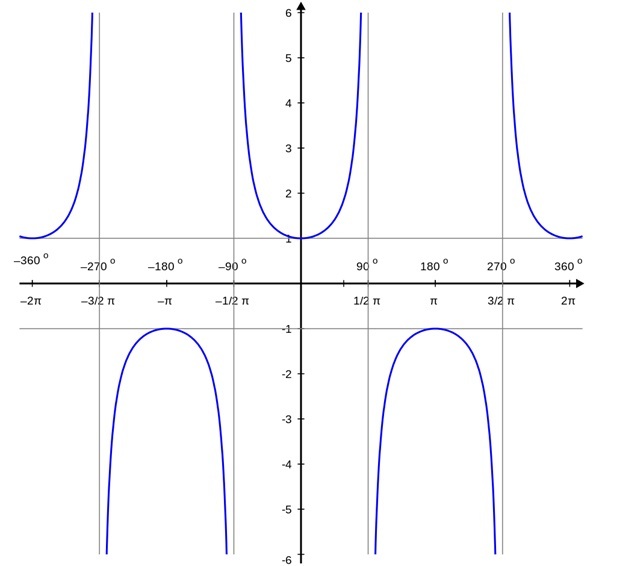
Secant Function and its Graph

In trigonometry, the secant function is periodic. The ratio of the hypotenuse's length to the base's length in a right-angled triangle is known as the secant function or sec function. It is also written as

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{Hypotenuse}{Base}}$$

since it is the reciprocal of the cosine function. Since we are already familiar with the cosine graph, graphing secant becomes extremely simple. By determining the reciprocal of each cosine value, we can quickly create the graph for $\mathrm{\sec\:x}$. When $\mathrm{\cos\:x}$ has a very small value, sec x will have a very large value. Specifically, determining1 𝑦 for each value of y along the line $\mathrm{y\:=\:\cos\:x}$. The following table displays some angles in radians −

x	cos x	sec x
0	1	1
$\mathrm{\frac{\pi}{6}}$	$\mathrm{\frac{\sqrt{3}}{2}}$	$\mathrm{\frac{2}{\sqrt{3}}}$
$\mathrm{\frac{\pi}{4}}$	$\mathrm{\frac{1}{\sqrt{2}}}$	$\mathrm{\sqrt{2}}$
$\mathrm{\frac{\pi}{3}}$	$\mathrm{\frac{1}{2}}$	2
$\mathrm{\frac{\pi}{2}}$	0	Not defined

Additionally, we notice that the secant function goes to infinity when the cosine function's value is zero, meaning the secant is undefined at that point. As a result, we get the sec x graph as follows −

Sec 0

One is the value of Sec 0 degrees. Sec 0 degrees is represented by $\mathrm{\sec\:(0°\:\times\:\frac{\pi}{180°})}$, often known as $\mathrm{\sec\:(0\pi)}$ or $\mathrm{\sec\:(0)}$. The positive x-axis contains the angle of 0°. Therefore, $\mathrm{\sec\:0°\:value\:=\:1}$.

$\mathrm{\sec\:(0°)}$ can be represented as $\mathrm{(\sec\:0°\:+\:n\:\times\:360°)}$, 𝑛 ∈ 𝑍. Since the secant function is a periodic function, $\mathrm{\sec\:0°\:=\:\sec\:360°\:=\sec\:720°}$, and so on.

Because secant is an even function, $\mathrm{\sec\:(-0°)}$ equals $\mathrm{\sec\:(0°)}$, which equals 1

Significance of Secant Function

One of the important trigonometric functions in trigonometry is the secant function. A straight line or ray that touches a curve, particularly a circle, more than once then it is equivalent to the right-angled triangle's hypotenuse to base ratio. The reciprocal of the cosine function is another name for the secant function.

Solved Examples

Example 1 − Find the value of secB in the following figure

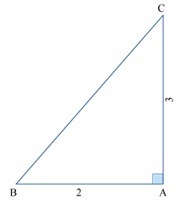
Solution − In the triangle, ABC the length of side AB and AC are 3 and 3 respectively and by the Pythagoras theorem, we get the length of BC as $\mathrm{\sqrt{3}}$

We know that the ratio of the hypotenuse's length to the base's length in a rightangled triangle is known as the secant function or sec function that is

$$\mathrm{\sec\:B\:=\:\frac{Hypotenuse}{Base}}$$

Now put the values, $\mathrm{\sec\:B\:=\:\frac{\sqrt{13}}{2}}$

Example 2 − Find the relation between $\mathrm{\cos\:2\theta\:and\:\sec\:\theta\:}$.

Solution − We know that the $\mathrm{\cos\:2\theta\:=\:cos^{2}\theta\:-\:sin^{2}\theta\:}$ and $\mathrm{\sin^{2}\theta\:+\:\cos^{2}\:\theta\:=\:1}$

$\mathrm{\:\:\:\Rightarrow\:sin^{2}\theta\:=\:1\:-\:\cos^{2}\:\theta\;}$

Now put this value in the above equation

$\mathrm{\:\:\:\:\:\:\cos\:2\theta\:=\:\cos^{2}\theta\:-\:(1\:-\:\cos^{2}\theta\:)}$

$\mathrm{\:\:\:\:\:\:\cos\:2\theta\:=\:2\cos^{2}\theta\:-\:1}$

we know that $\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta\:}}$ put this value in above equation.

$\mathrm{\:\:\:\:\:\:\cos\:2\theta\:=\:\frac{2}{\sec^{2}\:\theta}\:-\:1}$

Example 3 − Find the value of $\mathrm{\tan\:45°\:+\:\cot\:45°}$

Solution − $\mathrm{\tan\:45°\:+\:\cot\:45°}$

Now put their values $\mathrm{\tan\:45°\:+\:\cot\:45°\:=\:1\:+\:1}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:2}$

Example 4 − Find the value of $\mathrm{\sin^{2}48°\:+\:\cos^{2}48°}$

Solution − Given equation is $\mathrm{\sin^{2}48°\:+\:\cos^{2}48°}$

Here we do not need to put their values because we know that the $\mathrm{\sin^{2}\theta\:+\:cos^{2}\theta\:=\:1}$ where 𝜃 can be any value so

$\mathrm{\sin^{2}48°\:+\:\cos^{2}48°\:=\:1}$

Example 5 − What is the domain of secant function?

Solution − The domain of the secant function is $\mathrm{R\:-\:(2n\:+\:1)\frac{\pi}{2}}$ where R is real numbers.

Example 6 − What is the range of the secant function?

Solution − The range of secant function is $\mathrm{(-\infty,\:-1]\cup[+1\:,+\infty)}$

Example 7 − Find the value of the $\mathrm{\tan\:\theta}$ when the value of $\mathrm{\sec\:\theta}$ is 2.

Solution − We know that the relation between $\mathrm{\tan\:\theta}$ and $\mathrm{\sec\:\theta}$ is

$$\mathrm{\sec^{2}\:\theta\:=\:1\:+\:\tan^{2}\:\theta}$$

$$\mathrm{\Rightarrow\:\tan^{2}\:\theta\:=\sec^{2}\:\theta\:-\:1}$$

It is given that the value of $\mathrm{\sec\theta}$ now put this value in the above equation,

$$\mathrm{\Rightarrow\:\tan^{2}\theta\:=\:2^{2}\:-\:1}$$

$$\mathrm{\Rightarrow\:\tan^{2}\theta\:=\:4\:-\:1}$$

$$\mathrm{\Rightarrow\:\tan^{2}\theta\:=\:3}$$

$$\mathrm{\tan\theta\:=\:\sqrt{3}}$$

Example 8 − Find the value of secA by using the secant function

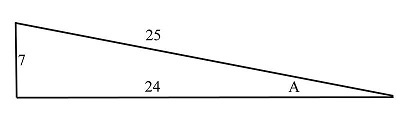
Solution − In this figure, the value of base, height, and the hypotenuse are 24, 7, and 25 respectively.

We know that the $\mathrm{\sec\:A\:=\:\frac{25}{24}}$

Example 9 − Find the value of $\mathrm{\cos\:\theta}$ when the value of $\mathrm{\sec\:\theta\:=\:2}$

Solution − We know that $\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta}\:=\:\frac{Hypotenuse}{Base}\:=\:\frac{Hypotenuse}{Base}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:cos\:\theta\:=\:\frac{1}{\sec\:\theta}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:cos\:\theta\:=\:\frac{1}{2}}$

Conclusion

The value of the secant trigonometric function for an angle of 0 degrees (Sec 0 degrees) is one. The ratio of the hypotenuse's length to the base's length in a right-angled triangle is known as the secant function or sec function. It is also written as

$\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta}\:=\:\frac{Hypotenuse}{Base}}$ since it is the reciprocal of the cosine function.

FAQs

1. What do you mean by Trigonometry?

The link between a right triangle's side ratio and angle is the subject of the mathematical branch of trigonometry.

2. What do you mean by sec function?

In trigonometry, the secant function is periodic. The ratio of the hypotenuse's length to the base's length in a right-angled triangle is known as the secant function or sec function

3. What is the relation between cos and sec function?

Sec function is also written as $\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta}\:=\:\frac{Hypotenuse}{Base}}$ because it is the reciprocal of the cosine function.

4. What is the value of the sec function at 0 degrees?

The value of the secant trigonometric function for an angle of 0 degrees (Sec 0 degrees) is one.

5. Find the nature (odd, even) of the secant function?

The secant function is an even function because $\mathrm{\sec(-x)\:=\:\sec\:x}$ for all x