Scalar triple product

Introduction

The scalar triple product is used to find the volume of parallelepiped, which is a 3 dimension of parallelogram. As it is a triple product it deals with the three vectors on the three adjacent edges starting from a common vertex.

$\mathrm{volume\:of\:parallelepiped\:=\:\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

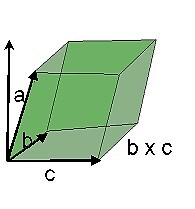
We know the area of base of parallelepiped is the area of a parallelogram $\mathrm{=\:l\:\times\:b}$

$\mathrm{Area\:of\:the\:base\:=\:\lvert\:\overrightarrow{b}\:\times\:\overrightarrow{c}\:\rvert}$

To find the height of the Parallelepiped, b × c is a perpendicular line drawn to b and c which is not the actual height of parallelepiped. We first consider the height of the cuboid and convert it into parallelepiped. The projection of $\mathrm{\overrightarrow{a}\:on\:\overrightarrow{b}\:\times\:\overrightarrow{c}}$ gives the height of parallelepiped.

$\mathrm{\overrightarrow{a}\:.\:\frac{(\overrightarrow{b}\:\times\:\overrightarrow{c})}{\:\lvert\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:\rvert}}$

Now to find the volume of parallelepiped

$\mathrm{Area\:of\:base\:\times\:height\:=\mathrm{\overrightarrow{a}\:.\:\frac{(\overrightarrow{b}\:\times\:\overrightarrow{c})}{\:\lvert\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:\rvert}\:\:\lvert\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:\rvert}}$

$\mathrm{volume\:of\:parallelepiped\:=\:\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

Vector

Many vectors are displacement vectors, denoting how far an object is travelled and in which direction. Vector deals with both magnitude and direction. A magnitude represents how much and direction represents the angle. A longer vector means greater magnitude. If a vector connects two vectors A and B we can write it as $\mathrm{\overrightarrow{AB}}$

Scalar or dot product

The multiplication of two vectors is called a scalar or dot product. When two vectors $\mathrm{\overrightarrow{A}\:and\:\overrightarrow{B}}$ multiplied we represent it using (•) that is $\mathrm{\overrightarrow{A}\:.\:\overrightarrow{B}}$. This can be read as the dot product of $\mathrm{\overrightarrow{A}\:and\:\overrightarrow{B}}$. The dot product is possible only for multiplying two vectors in the same dimension.

For example

Consider two vectors $\mathrm{A\:=\:(p,q,r)\:and\:B\:=\:(u,v,w)}$

Solution

To find the dot product of A and B, multiply the x component of A to x component of B

$\mathrm{A\:.\:B\:=\:(pu)\:+\:(qv)\:+\:(rw)}$

The dot product always results only in the numbers.

when the angle 𝛳 lies between the $\mathrm{\overrightarrow{a}\:and\:\overrightarrow{b}}$, to find the dot product,

$\mathrm{a\:.\:b\:=\:\lvert\:a\:\rvert\:\lvert\:b\:\rvert\:\cos\:\theta}$

$\mathrm{\cos\:\theta\:=\:\frac{a\:.\:b}{\lvert\:a\:\rvert\:\lvert\:b\:\rvert}}$

where $\mathrm{\lvert\:a\:\rvert\:\:and\:\lvert\:b\:\rvert\:}$ are magnitudes.

Vector or cross product

Let a vector A and vector B be the two vectors, the vector or cross product results in the perpendicular line. The cross is represented by the symbol (×) i. e.,$\mathrm{A\:\times\:B}$. In cross product, the order of multiplication is important which means $\mathrm{A\:\times\:B\neq\:B\:\times\:A}$

For example

If $\mathrm{\overrightarrow{A}\:=\:x_{1}\widehat{i}\:+\:y_{1}\widehat{j}\:+\:z_{1}\widehat{k}\:and\:\overrightarrow{B}\:=\:x_{2}\widehat{i}\:+\:y_{2}\widehat{j}\:+\:z_{2}\widehat{k}}$ Calculate $\mathrm{\overrightarrow{A}\:\times\:\overrightarrow{B}}$

Solution

Given $\mathrm{\overrightarrow{A}\:=\:x_{1}\widehat{i}\:+\:y_{1}\widehat{j}\:+\:z_{1}\widehat{k}}$

$\mathrm{\overrightarrow{B}\:=\:x_{2}\widehat{i}\:+\:y_{2}\widehat{j}\:+\:z_{2}\widehat{k}}$

To find the cross product, use the determinant

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ x_{1} & y_{1} & z_{1}\\ x_{2} & y_{2} & z_{2}\end{vmatrix}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\widehat{i}\:(y_{1}z_{2}\:-\:y_{2}z_{1})\:-\:\widehat{j}\:(x_{1}z_{2}\:-\:x_{2}z_{1})\:\widehat{k}\:(x_{1}y_{2}\:-\:x_{2}y_{1})}$

Scalar triple product

Consider the three vectors $\mathrm{\overrightarrow{A}\:=\:x_{1}\widehat{i}\:+\:x_{2}\widehat{j}\:+\:x_{3}\widehat{k}\:,\:\overrightarrow{B}\:=\:y_{1}\widehat{i}\:+\:y_{2}\widehat{j}\:+\:y_{3}\widehat{k}\:,\:\overrightarrow{C}\:=z_{1}\widehat{i}\:+\:z_{2}\widehat{j}\:+\:z_{3}\widehat{k}}$ find the scalar triple product

Solution

To find the scalar triple product,

$\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})}$

$\mathrm{\widehat{B}\:\times\:\widehat{C}\:=}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ y_{1} & y_{2} & y_{3}\\ z_{2} & z_{2} & z_{3}\end{vmatrix}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\widehat{i}\:(y_{2}z_{3}\:-\:y_{3}z_{2})\:-\:\widehat{j}\:(y_{1}z_{3}\:-\:y_{3}z_{1})\:\widehat{k}\:(y_{1}z_{2}\:-\:y_{2}z_{1})}$

now

$\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})}$

$\mathrm{(x_{1}\widehat{a}\:+\:x_{2}\widehat{j})\:.\:(\widehat{i}(y_{2}z_{3}\:-\:y_{3}z_{2})\:\:-\:\widehat{j}(y_{1}z_{3}\:-\:y_{3}z_{1})\:+\:\widehat{k}(y_{1}z_{2}\:-\:y_{2}z_{1})}$

$\mathrm{(x_{1}(y_{2}z_{3}\:-\:y_{3}z{2})\:+\:x_{2}(y_{1}z_{3}\:-\:y_{3}z_{1})\:+\:x_{2}(y_{1}z_{2}\:-\:y_{2}z_{1}))}$

The scalar triple product is $\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})\:=}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{vmatrix} x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3}\\ z_{2} & z_{2} & z_{3} \end{vmatrix}}$

Coplanarity of three vectors

The vectors A, B, C lie in the same plane, the volume of the parallelepiped is zero.

If $\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})\:=\:0}$ Then the three vectors are coplanar.

Solved examples

1. Find the dot product of A and B if $\mathrm{A\:=\:4\widehat{i}\:+\:3\widehat{j}}$ and $\mathrm{B\:=\:3\widehat{i}\:+\:11\widehat{j}}$

Solution

$\mathrm{(\overrightarrow{A}\:.\:\overrightarrow{B})\:=\:(4\:\times\:3)\:+\:(3\:\times\:11)}$

$\mathrm{=\:45}$

2. Find the angle between $\mathrm{u\:=\:\widehat{i}\:+\:2\widehat{j}\:and\:v\:=\:2\widehat{i}\:+\:\widehat{j}}$

Solution

$\mathrm{\cos\:\theta\:=\:\frac{u\:.\:v}{\lvert\:u\:\rvert\:\lvert\:v\:\rvert\:}}$

$\mathrm{u\:.\:v\:=\:2(1)\:+\:(2)1\:+\:4}$

$\mathrm{\lvert\:u\:\rvert\:=\:\sqrt{(1^{2})\:+\:(2^{2})}\:=\:\sqrt{1\:+\:4}\:=\:\sqrt{5}}$

$\mathrm{\lvert\:v\:\rvert\:=\:\sqrt{(2^{2})\:+\:(1^{2})}\:=\:\sqrt{4\:+\:1}\:=\:\sqrt{5}}$

$\mathrm{\cos\:\theta\:=\:\frac{4}{\sqrt{5}\:.\:\sqrt{5}}}$

$\mathrm{\theta\:=\:\cos^{-1}(\frac{4}{5})}$

3. Find the cross product of $\mathrm{A\:=\:3\widehat{i}\:+\:2\widehat{j}\:-\:5\widehat{k}}$ and $\mathrm{2\widehat{i}\:-\:6\widehat{j}\:+\:9\widehat{k}}$

Solution

$$\mathrm{\begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ 3 & 2 & -1\\ 2 & -6 & 9 \end{vmatrix}}$$

$\mathrm{\widehat{i}((2)(9)\:-\:(-5)(-6))\:-\:\widehat{j}(3)(9)\:-\:(2)(-5)\:+\:\widehat{k}((3)(-6)\:-\:(2)(2))}$

$\mathrm{=\:\widehat{i}(18\:-\:30)\:-\:\widehat{j}(27\:+\:10)\:+\:\widehat{k}(-18\:-\:4)}$

$\mathrm{=\:-(1\widehat{i}\:+\:37\widehat{j}\:+\:22\widehat{k})}$

4. Check whether the given vectors are coplanar, find $\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$ if

$\mathrm{A\:=\:2\widehat{i}\:+\:\widehat{j}\:+\:3\widehat{k}\:,\:B\:=\:\widehat{i}\:+\:3\widehat{j}\:+\:\widehat{k}\:,\:C\:=\:2\widehat{i}\:+\:2\widehat{j}\:+\:\widehat{k}}$

Solution

$\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

$$\mathrm{\begin{vmatrix} 2 & 1 & 3 \\ 1 & 3 & 1\\ 2 & 2 & 1 \end{vmatrix}}$$

$\mathrm{=\:2(3\:-\:2)\:-1(1\:-\:2)\:+\:3(2\:-\:6)}$

$\mathrm{=\:2(1)\:-\:1(-1)\:+\:3(-4)}$

$\mathrm{=\mathrm{2\:+\:1\:-12\:=\:-9}}$

The scalar triple product is not coplanar.

Find the scalar triple product, if $\mathrm{A\:=\widehat{i}\:+\:2\widehat{j}\:+\:\widehat{k}\:;\:B\:=\:2\widehat{i}\:+\:\widehat{j}\:+\:3\widehat{k}\:;\:C\:=\:3\widehat{i}\:+\:3\widehat{j}\:\widehat{k}}$

Solution

$\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

$$\mathrm{\begin{vmatrix} 1 & 2 & 1 \\ 2 & 1 & 3\\ 3 & 3 & 1 \end{vmatrix}}$$

$\mathrm{=\:-8\:-\:14\:+\:3\:=\:19}$

Conclusion

Scalar triple product is 3-dimensional measurement used to find the volume of parallelepiped. The cross product is represented in matrix form by taking determinants. The dot product is direct multiplication; it also measures the angle between the vectors.

FAQs

1. Do the cyclic permutations affect the scalar triple product?

No, the cyclic permutations of three vectors a, b and c doesn't affect the scalar product it remains the same.

$\mathrm{[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]\:=\:[\overrightarrow{b},\overrightarrow{a},\overrightarrow{c}]\:=\:[\overrightarrow{c},\overrightarrow{a},\overrightarrow{b}]}$

2. What happens to the scalar triple product when the dot and cross product interchanged?

When the dot and cross product interchanged, the value of the scalar triple product remains the same

i.e., $\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:=\:(\overrightarrow{a}\:\times\:\overrightarrow{b})\:.\:\overrightarrow{c}}$

3. What will change in a scalar triple product if any two values change its position?

When the position of any two vectors changes it will become negative

i.e., $\mathrm{[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]\:=\:-\:[\overrightarrow{b},\overrightarrow{a},\overrightarrow{c}]}$

4. What happens, when the two vectors repeat in a scalar triple product?

when two vectors repeat, the scalar triple product will be zero which is i e.,

$\mathrm{[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]\:,\:[\overrightarrow{b},\overrightarrow{b},\overrightarrow{c}]\:,\:[\overrightarrow{a},\overrightarrow{c},\overrightarrow{c}]}$

i.e., $\mathrm{[\overrightarrow{a},\overrightarrow{a},\overrightarrow{c}]\:=\:\overrightarrow{a}\:.\:(\overrightarrow{a}\:\times\:\overrightarrow{c})\:=\:0}$

$\mathrm{[\overrightarrow{b},\overrightarrow{b},\overrightarrow{c}]\:=\:\overrightarrow{b}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:=\:0}$

5. What happens, when all the vectors are the same in a scalar triple product?

when all the three vectors are the same, the scalar triple product will be zero which is i.e., $\mathrm{[\overrightarrow{a},\overrightarrow{a},\overrightarrow{a}]}$

i.e., $\mathrm{[\overrightarrow{a},\overrightarrow{a},\overrightarrow{a}]\:=\:\overrightarrow{a}\:.\:(\overrightarrow{a}\:\times\:\overrightarrow{a})\:=\:0}$