Quality Factor of Inductor and Capacitor

A parameter of an oscillatory system, such as an ac circuit, which expresses the relationship between stored energy and energy dissipation is known as quality factor of the system. The quality factor is also called as Q-factor.

Mathematically, the quality factor or Q-factor of an ac circuit is given by the ratio of the maximum electrical energy stored in the circuit to the energy dissipated in one time period, i.e.,

$$\mathrm{ Q \: Factor =\frac{2\pi \times maximum\: energy \: stored\: per\: cycle}{Energy\: dissipated\: per\: cycle} } $$

The quality factor (Q-factor) can be defined for those circuits only that contain energy storing elements. In ac circuits, there are two energy storing elements namely inductor and capacitor. Thus, in this article, we will discuss the quality factor of inductor and capacitor.

Quality Factor of an Inductor

An inductor is a passive circuit element that stores electrical energy in the form of magnetic field. The property by which an inductor stores the energy in the magnetic field is known as inductance.

An inductor is constructed by twisting a conducting wire into a coil. Ideally, an inductor must have very high inductance and zero resistance, but a real or practical inductor has a small resistance in addition to its inductance. Hence, to have a better quality inductor, the value of the resistance of the inductor should be lower as much as possible.

The low value of resistance and high value of inductance of the inductor indicate that the maximum value of energy stored in the inductor per cycle is greater than the energy dissipated per cycle. Such an inductor has high quality factor.

For a given operating frequency, the quality factor or Q-factor of an inductor is defined as the ratio of maximum energy stored in the inductor to the energy dissipated per cycle, i.e.

$$\mathrm{ Q \: Factor =\frac{I^{2}X_{L}}{I^{2}R}=\frac{X_{L}}{R} =\frac{\omega L}{R}} $$

Where, L is the inductance of the inductor, and R is the resistance of the inductor.

Hence, the quality factor of an inductor is given by the inductive reactance divided by the resistance of the inductor.

Quality Factor is a Dimensionless Quantity

The unit of XL and R is the same, i.e., Ohm. Hence, the quality factor is a dimensionless quantity.

Now, let us prove the above expression of quality factor of an inductor.

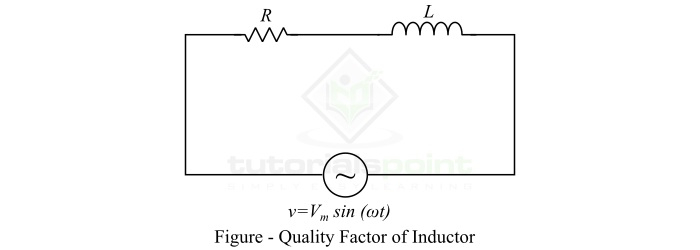
Consider an inductor having an inductance of L Henry and a resistance of R ohms. It is connected across an AC voltage source of V volts whose angular frequency is ω radians per second. Let the maximum current through the circuit is I_m.

Then, the maximum energy stored in the inductor is given by,

$$\mathrm{W_{m}=\frac{1}{2}LI_{m}^{2}}$$

Also, the energy dissipated in the inductor due to its resistance in one cycle is given by,

$$\mathrm{W_{d}=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\, RT=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\times R\times \frac{1}{f}}$$

Where, T is the time period of the ac voltage.

Thus, by the definition of quality factor, we get,

$$\mathrm{Q\: Factor=\frac{2\pi \times \left ( \frac{1}{2}LI_{m}^{2} \right )}{\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\times R\times \frac{1}{f}}}$$

$$\mathrm{\Rightarrow Q\: Factor=\frac{2\pi fL}{R}=\frac{\omega L}{R}= \frac{X_{L}}{R}}$$

Hence, this is the quality factor of an inductor.

Quality Factor of a Capacitor

A capacitor is also a circuit element that stores electrical energy in the form of electrostatic energy. An ideal capacitor is supposed to have zero resistance and very high capacitance. But, a practical capacitor has a small resistance in addition to its capacitance. The value of this resistance should be lower for the better quality of the capacitor.

A capacitor is designed for storing energy, but it also dissipates some part of input energy due to internal resistance. The parameter that gives information about the quality of the capacitor is referred to as the quality factor of the capacitor.

For an operating frequency of ω rad/sec, the quality factor of a capacitor is defined as the ratio of maximum energy stored to the energy dissipated in the capacitor in one cycle, i.e.,

$$\mathrm{Q\: Factor=\frac{I^{2}X_{c}}{I^{2}R}=\frac{X_{c}}{R}=\frac{1}{\omega CR}}$$

Where, 𝑋_𝐶 is the capacitive reactance and R is the resistance of the capacitor.

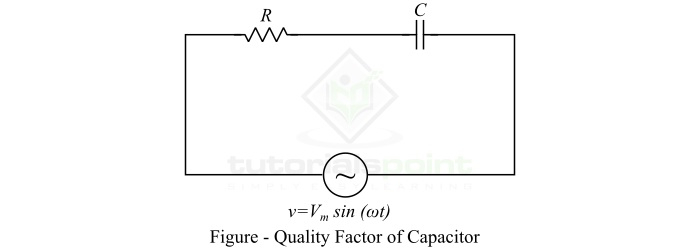
Consider a capacitor of capacitance C Farad having a resistance of R Ohms. It is connected across an AC voltage source of V volts.

If 𝑉_𝑚 is the maximum value of the voltage of the source, then the maximum energy stored in the capacitor is given by,

$$\mathrm{W_{m}=\frac{1}{2}CV_{m}^{2}}$$

But, R << X_C, thus,

$$\mathrm{V_{m}=I_{m}X_{c}=\frac{I_{m}}{\omega C}}$$

Therefore, the maximum energy stored in the capacitor per cycle is given by,

$$\mathrm{W_{m}=\frac{1}{2}\left ( \frac{I_{m}^{2}}{\omega ^{2}C} \right )}$$

And, the energy dissipated in the capacitor due to its resistance in one cycle is given by,

$$\mathrm{W_{d}=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\,RT=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2} R\times \frac{1}{f}}$$

Hence, the quality factor of the capacitor will be,

$$\mathrm{Q\: Factor=2\pi \times \left [ \frac{\frac{1}{2}\left ( \frac{I_{m}^{2}}{\omega ^{2}C} \right )}{\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\, R\times \frac{1}{f}} \right ]=\frac{1}{\omega RC}=\frac{X_{C}}{R}}$$

Hence, this is the quality factor of the capacitor.

Numerical Example (1)

A real inductor having an inductance of 2 mH and a resistance of 1 Ω is connected to an AC voltage source of 50 Hz frequency. Determine the quality factor of the inductor.

Solution

Given data,

• Inductance, 𝐿 = 2 mH = 2 × 10⁻³H
• Resistance, 𝑅 = 1 Ω
• Frequency, 𝑓 = 50 Hz

Hence, the quality factor of the inductor is

$$\mathrm{Q\: Factor=\frac{2\pi fL}{R}=\frac{2\pi \times 50\times 2\times 10^{-3}}{1}=0.628}$$

Numerical Example (2)

A capacitor of 3 μF has a resistance of 1.5 Ω and is connected across an ac source of 50 Hz frequency. Determine the quality factor of the capacitor.

Solution

Given data,

• Capacitance, 𝐶 = 3 μF = 3 × 10⁻⁶ F
• Resistance, 𝑅 = 1.5 Ω
• Frequency, 𝑓 = 50 Hz

Thus, the quality factor of the capacitor is given by,

$$\mathrm{Q\: Factor=\frac{1}{2\pi fRC}=\frac{1}{2\pi \times 50\times 1.5\times3\times 10^{-6}}}$$

$$\mathrm{\therefore Q\: Factor=0.001413}$$

Conclusion

From the above discussion, we may conclude that an inductor will have high quality factor, if its resistance is very much less than its reactive inductance. The high quality factor of the inductor indicates that it will store more amount of energy and dissipate much lesser energy in one cycle of the ac power supply.

Similarly, a capacitor is considered of high quality, if it has the capacitive reactance more than its resistance so that it dissipates only a small amount of energy.