Charging of a Capacitor – Formula, Graph, and Example

A capacitor is a passive circuit component used in electrical and electronic circuits to introduce capacitance. The capacitance is defined as the property of a substance by which it stores electrical energy in the form of electrostatic field.

A typical capacitor consists of two metal plates which are separated by a dielectric material. It is the dielectric material that has ability to store electrical energy in the form of electrostatic charge.

The process of storing electrical energy in the form of electrostatic field when the capacitor is connected to a source of electrical energy is known as charging of capacitor. This stored energy in the electrostatic field can be delivered to the circuit at a later point of time.

In this article, we will discuss the charging of a capacitor, and will derive the equation of voltage, current, and electric charged stored in the capacitor during charging.

What is the Charging of a Capacitor?

As discussed earlier, the charging of a capacitor is the process of storing energy in the form electrostatic charge in the dielectric medium of the capacitor.

Consider an uncharged capacitor having a capacitance of C farad. This capacitor is connected to a dc voltage source of V volts through a resistor R and a switch S as shown in Figure-1.

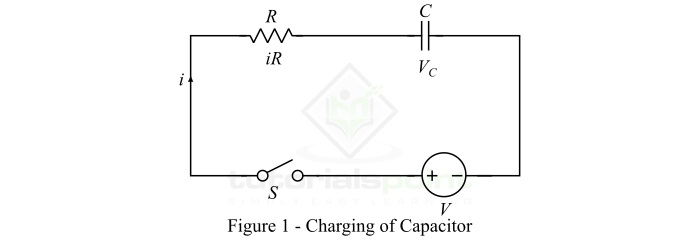
When the switch S is closed, the capacitor starts charging, i.e. a charging current starts flowing through the circuit. This charging current is maximum at the instant of switching and decreases gradually with the increase in the voltage across the capacitor. Once the capacitor is charged to a voltage equal to the source voltage V, the charging current will become zero.

Hence, to understand the charging of the capacitor, we consider the following two instants −

Instant 1 − When switch is closed

At the switching instant, the voltage across the capacitor is zero because initially we taken a fully uncharged capacitor. At this instant, the entire source voltage V is dropped across the resistor R, and the charging current is maximum (say I_m).

Therefore,

$$\mathrm{Initial\: charging\: current,\, I_{m}=\frac{V}{R}}$$

$$\mathrm{Voltage\: across\: capacitor, V_{C} = 0}$$

$$\mathrm{Charge\: on\: capacitor, Q_{C} = 0}$$

Instant 2: Any Instant "t"

After having closed the switch S, the voltage across the capacitor starts increasing and the charging current in the circuit starts decreasing gradually. Let at any instant of time t during charging of the capacitor,

$$\mathrm{Charging\: current = i}$$

$$\mathrm{Voltage\: across\: capacitor, V_{C} = v}$$

$$\mathrm{Charge\: on\: capacitor, Q_{C} = q = Cv}$$

Now, applying KVL in the circuit, we can write,

$$\mathrm{V=v+iR\: \cdot \cdot \cdot (1)}$$

$$\mathrm{\because Current\: in\: capacitor,\, i=C\frac{dv}{dt}}$$

$$\mathrm{\therefore V=v+CR\frac{dv}{dt}}$$

Rearranging the equation, we get,

$$\mathrm{\frac{dv}{V-v}=\frac{dt}{RC}}$$

Integrating on both sides, we get,

$$\mathrm{\int \frac{dv}{V-v}=\int \frac{dt}{RC}}$$

$$\mathrm{\because \int \frac{dx}{1-x}=-log_{e}\left|1-x \right|}$$

Using this integration identity, we get,

$$\mathrm{-log_{e}\left ( V-v \right )=\frac{t}{RC}+K}$$

Where, K is a constant whose value can be determined from the initial conditions of the capacitor. Thus, at t = 0, v = 0.

$$\mathrm{\therefore K=-log_{e}V }$$

Substituting this value of K in the above expression, we get,

$$\mathrm{-log_{e}\left ( V-v \right )=\frac{t}{RC}-log_{e}V}$$

$$\mathrm{\Rightarrow log_{e}\left ( V-v \right )-log_{e}V=-\frac{t}{RC}}$$

$$\mathrm{\Rightarrow log_{e}\left ( \frac{V-v}{V} \right )=-\frac{t}{RC}}$$

Taking antilog on both sides, we get,

$$\mathrm{\Rightarrow \frac{V-v}{V}=e^{-\frac{t}{RC}}}$$

On rearranging this equation, we get,

$$\mathrm{v=V\left ( 1-e^{-\frac{t}{RC}} \right )\: \cdot \cdot \cdot \left ( 2 \right )}$$

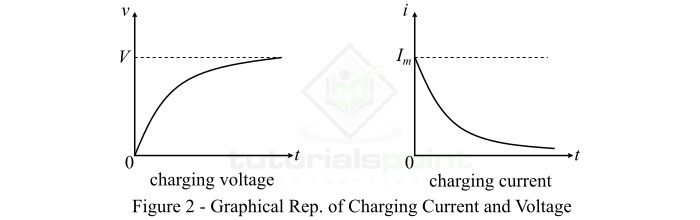
The expression in equation (2) gives the voltage across a capacitor at any time t. It shows that the increase in voltage across a capacitor during charging follows an exponential law.

Equation (2) also indicates that as t increases, the exponential term e^-t/RC gets reduced and voltage across the capacitor increases. When the term e^-t/RC becomes zero, the voltage across the capacitor will become equal to the source voltage V, and the capacitor is said to be fully charged. When the capacitor is fully charged, the voltage drop across the resistor R is zero.

Charge on the Capacitor

If the charge on the capacitor is q at any time instant t, and that is Q when the capacitor is fully charged. For a capacitor, we have,

$$\mathrm{v=\frac{q}{C}\: and\: V=\frac{Q}{C}}$$

Then, from equation (2), we have,

$$\mathrm{\frac{q}{C}=\frac{Q}{C}\left ( 1-e^{-\frac{t}{RC}} \right )}$$

$$\mathrm{\therefore q=Q\left ( 1-e^{-\frac{t}{RC}} \right )\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

It indicates that the charge on the plates of a capacitor increases exponentially during charging.

Charging Current of Capacitor

From equation (1), we have,

$$\mathrm{V-v=iR\: \: \cdot \cdot \cdot \left ( 4 \right )}$$

And from equation (2), we have.

$$\mathrm{V-v=Ve^{-\frac{t}{RC}}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$

Therefore,

$$\mathrm{iR=Ve^{-\frac{t}{RC}}}$$

$$\mathrm{\Rightarrow i=\frac{V}{R}e^{-\frac{t}{RC}}}$$

$$\mathrm{\therefore i=I_{m}e^{-\frac{t}{RC}}\: \: \cdot \cdot \cdot \left ( 6 \right )}$$

Where, I_m is the initial charging current. From equation (6), it is clear that the charging current of a capacitor decreases exponentially during the charging process of the capacitor.

Graphical Representation of Charging of a Capacitor

The graphical representation of the charging voltage and current of a capacitor are shown in Figure-2.

Numerical Example

A 5 μF capacitor is connected in series with 1 MΩ resistor across 250 V supply. Calculate: initial charging current, and the charging current and voltage across the capacitor 5 seconds after it is connected to the supply.

Solution

Given data,

• Capcitance, C = 5 μF
• Series resistance, R = 1 MΩ
• Supply voltage, V = 250 V

Initial Charging Current

$$\mathrm{I_{m}=\frac{V}{R}=\frac{250}{1}=250\, \mu A}$$

Charging current after 5 seconds

$$\mathrm{i=I_{m}e^{\frac{t}{RC}}=250\times e^{\left ( \frac{-5}{1\times 10^{6}\times 5\times10^{-6}} \right )} }$$

$$\mathrm{i=250\times 0.367=91.75\, \mu A }$$

Voltage across capacitor after 5 seconds

$$\mathrm{v=V\left ( 1-e^{-\frac{t}{RC}} \right )}$$

$$\mathrm{\Rightarrow v=250 \left [ 1-e^{\left ( \frac{-5}{1\times 10^{6}\times 5\times10^{-6}} \right )} \right ] }$$

$$\mathrm{\Rightarrow v=250 \times 0.633 = 158.25 V }$$

Conclusion

From the above discussion, we can conclude that during charging of a capacitor, the charge and voltage across the capacitor increases exponentially, while the charging current decreases. A charged capacitor stores electrical energy in the form of electrostatic charge in the dielectric medium between the plates of the capacitor.