Quadrilateral: Angle Sum Property

Introduction

A quadrilateral in geometry is a four-sided polygon with four sides and four corners (vertices).

The Latin words Quadra, a variation of four, and latus, meaning "side," are the source of the name.

In reference to other polygons, it is also known as a tetragon, from the Greek "tetra" for "four" and "gon" for "corner" or "angle" (e.g. pentagon). Since "gon" is an anagram for "angle," it is also known as a quadrangle or 4-angle.

There are two types of quadrilaterals: simple (not self-intersecting) and complex (self-intersecting, or crossed).

Convex or concave quadrilaterals are simple quadrilaterals. In this tutorial, we discuss quadrilaterals and their types along with properties.

Quadrilaterals

A quadrilateral is a closed object in geometry that is created by connecting four points, any three of which are not collinear. There are 4 sides, 4 angles, and 4 vertices in a quadrilateral. A quadrilateral may or may not have equal sides on all four sides. The arrangement of the vertices must be taken into consideration whenever a quadrilateral is named. The following quadrilateral, for instance, should be referred to as PQRS, QRSP, PSRQ, or RSPQ. Since they alter the order of vertices in which a quadrilateral is generated, it cannot be termed PRSQ or SQPR. A quadrilateral with the letters PQRS has four sides: PQ, QR, RS, and PS, as well as two diagonals: PR and QS.

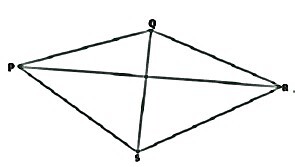
The aforementioned quadrilaterals each have unique characteristics. Nevertheless, all quadrilaterals have a few characteristics. They are listed below;

• There are four sides of them.

• There are four angle of them.

• There are four vertices of them.

• There are two diagonals in them.

• 360° is the total of all interior angles.

We shall thoroughly examine the additional characteristics of several quadrilaterals. The following characteristics of quadrilaterals can be used to identify a quadrilateral.

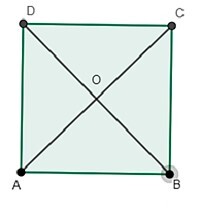
Properties of Square

Following is the geometrical figure square ABCD in which AB=BC=CD=AD & AC=BD.

that is all edges are equal and diagonals are equal and each angle is of measure 90 degrees i.e. $\mathrm{\angle A=\angle B=\angle C=\angle D=90^\circ}$

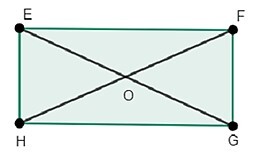
Properties of Rectangle

Following is the geometrical figure rectangle EFGH in which EF=GH & FG=EH & EG=FH.

that is opposite edges are equal and diagonals are equal and each angle is of measure 90 degrees $\mathrm{\angle E=\angle F=\angle G=\angle H=90^\circ}$

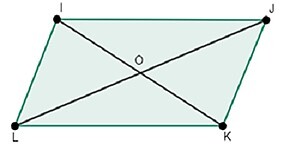
Properties of Parallelogram

Following is the geometrical figure parallelogram IJKL in which IJ=LK & JK=IL

$$\mathrm{IJ\parallel LK,JK\parallel IL}$$

that is opposite edges are equal and parallel and diagonals are bisectors of each other, they intersect at the point O. In parallelogram opposite angles are of the same measure i.e. $\mathrm{\angle I=\angle K\:\: \& \:\: \angle J=\angle L}$

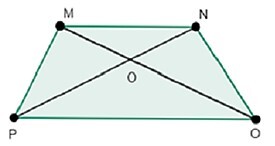
Properties of Trapezium

Following is the geometrical figure Trapezium MNOP in which

$$\mathrm{MN\parallel PO}$$

that is one pair of opposite edges are parallel and these two edges are called bases and the other two edges are called legs when lengths of legs same then that trapezium is called an isosceles trapezium

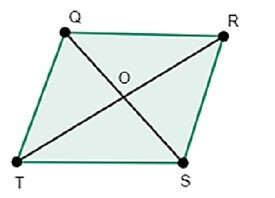
Properties of Rhombus

Following is the geometrical figure rhombus QRST in which $\mathrm{QR=RS=ST=QT\:\: \&\:\: QR\parallel TS,QT\parallel RS}$

that is all edges are equal in length and pairs of opposite edges are parallel and diagonals bisect each other at the point O. In rhombus opposite angles are of the same measure i.e. $\mathrm{\angle Q=\angle S\:\: \&\:\: \angle R=\angle T}$

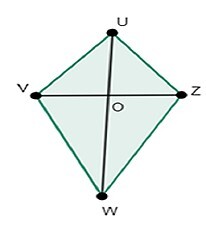
Properties of Kite

Following is the geometric figure kite UVWZ in which UV=UZ,VW=ZW

that is adjacent edges are equal in length and diagonals bisect each other at the point O.

Angle sum Property of a Quadrilateral

This property states that the sum of all angles of a quadrilateral is 360°.

Proof

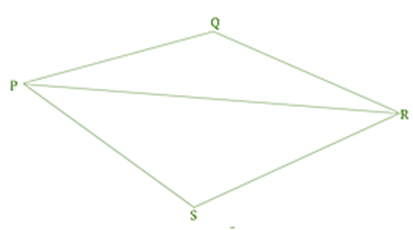
PQRS is a quadrilateral and PQ, QR, RS and PR are its four sides and PR is one of the diagonal of this quadrilateral PQRS

Due to diagonal PR the quadrilateral PQRS is now divided into two regions which are triangles PSR and PQR.

We know the angle sum property of a triangle which states that the sum of three angles in a triangle is 180 degrees.

Using this property of triangles in triangle PSR and triangle PQR we get following equations

$$\mathrm{\angle PQR+\angle QPR+\angle QRP=180^\circ………………….. (1)}$$

$$\mathrm{\angle PSR+\angle SPR+\angle SRP=180^\circ……………………. (2)}$$

Adding Equations (1) and (2) we get,

$$\mathrm{\angle PQR+\angle QPR+\angle QRP+\angle PSR+\angle SPR+\angle SRP=180^\circ+180^\circ=360^\circ…… (3)}$$

Note that;

$$\mathrm{\angle QPR+\angle SPR=\angle P}$$

$$\mathrm{\angle QRP+\angle SRP=\angle R}$$

$$\mathrm{\angle PQR=\angle Q\:\: \&\:\: \angle PSR=\angle S}$$

Thus, equation (3) becomes;

$$\mathrm{\angle P+\angle Q+\angle R+\angle S=360^\circ}$$

Hence, we proved that the sum of all angles in a quadrilateral is 360 degrees.

Solved Examples

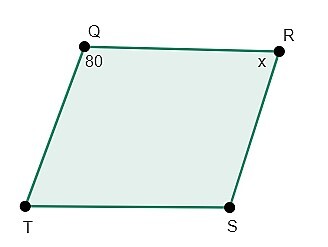
1.Find the measure of unknown angle x in the following quadrilateral which is rhombus.

Solution −

We know that opposite angles in a rhombus are of equal measure. Thus,

$$\mathrm{\angle Q=\angle S=80^\circ \:\:\&\:\: \angle R=\angle T=x}$$

Since the sum of four angles in quadrilaterals is 360 degrees, thus $\mathrm{\angle Q+\angle R+\angle S+\angle T=360^\circ}$

$$\mathrm{80+x+80+x=360^\circ}$$

$$\mathrm{2x+160=360}$$

$$\mathrm{2x=200}$$

$$\mathrm{x=100}$$

2.Determine the measure of angle y in the following parallelogram IJKL

Solution:

We know that opposite angles in a parallelogram are of equal measure. Thus, $\mathrm{\angle I=\angle K=110^\circ \:\:\&\:\: \angle J=\angle L=x}$

Since the sum of four angles in quadrilaterals is 360 degrees, thus $\mathrm{\angle I+\angle J+\angle K+\angle L=360^\circ}$

$$\mathrm{110+x+110+x=360^\circ L}$$

$$\mathrm{2x+220=360}$$

$$\mathrm{2x=140}$$

$$\mathrm{x=70}$$

3.Determine the value of y in the following rectangle EFGH.

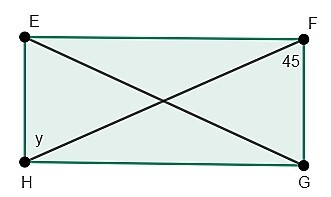
Solution:

In the rectangle each angle is of measure 90 degrees and pairs of opposite sides are equal and parallel.

We have $\mathrm{ EF\parallel HG}$

Therefore,

$\mathrm{ \angle EHO= \angle OFG…………….}$ (alternate angles are equal)

Thus,

$$\mathrm{y=45^o}$$

Conclusion

A closed quadrilateral has four sides, four vertices, and four angles. It is a form of polygon. In order to create it, four non-collinear points are joined. Quadrilaterals always have a total internal angle of 360 degrees.

FAQs

1. What makes quadrilaterals unique?

There are numerous unique properties in peculiar quadrilaterals. There is only one set of parallel sides in a trapezoid. Two sets of equally parallel sides make up a parallelogram. A parallelogram with four right angles is a rectangle.

2. What connections do quadrilaterals have to one another?

There are many different kinds of quadrilaterals, but they all have four sides, two diagonals, and internal angles that add up to 360 degrees. They are all connected to one another, but they are all unique and have various characteristics.

3. Quadrilaterals are all parallelograms, right?

Incorrect. Since every parallelogram is a quadrilateral, any parallelogram is a quadrilateral.

4. Are quadrilaterals always polygons?

A quadrilateral must always have four sides, and four angles and the sides cannot be curved (because it is a type of polygon). Therefore, a polygon is not always a quadrilateral, but a quadrilateral is always a polygon.

5. Are a quadrilateral's four sides equal in size?

Both regular and irregular quadrilaterals exist. A regular quadrilateral must have four equal sides, four equal angles, and diagonals that cross each other in a bisecting direction. The only quadrilateral that meets each of these requirements is the square.