
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Python Program for nth Catalan Number
In this article, we will learn about calculating the nth Catalan number.
Catalan numbers are a sequence of natural numbers that are defined by the recursive formula −
$$C_{0}= 1\:and\:C_{n+1}=\displaystyle\sum\limits_{i=0}^n C_{i}C_{n-i} for \:n\geq0;$$
The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132,429,...................
Catalan numbers can be obtained both by recursion and dynamic programming. So let’s see their implementation.
Approach 1: Recursion Method
Example
# A recursive solution def catalan(n): #negative value if n <=1 : return 1 # Catalan(n) = catalan(i)*catalan(n-i-1) res = 0 for i in range(n): res += catalan(i) * catalan(n-i-1) return res # main for i in range(6): print (catalan(i))
Output
1 1 2 5 14 42
The scope of all the variables and recursive calls are shown below.
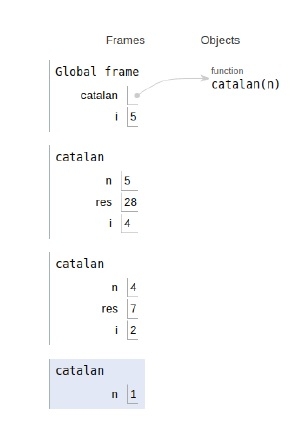
Approach 2: Dynamic Programming Method
Example
# using dynamic programming def catalan(n): if (n == 0 or n == 1): return 1 # divide table catalan = [0 for i in range(n + 1)] # Initialization catalan[0] = 1 catalan[1] = 1 # recursion for i in range(2, n + 1): catalan[i] = 0 for j in range(i): catalan[i] = catalan[i] + catalan[j] * catalan[i-j-1] return catalan[n] # main for i in range (6): print (catalan(i),end=" ")
Output
1 1 2 5 14 42
The scope of all the variables and recursive calls are shown below.
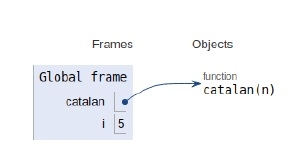
Conclusion
In this article, we learned about the method of generating the nth Catalan number.

Advertisements