Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C/C++ Program for nth Catalan Number?
Catalan numbers are a sequence of numbers. Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involving recursively-defined objects.
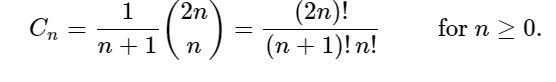
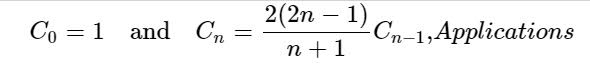
Cn is the number of Dyck words of length 2n. A Dyck word is a string consisting of n X's and n Y's such that no initial segment of the string has more Y's than X's. For example, the following are the Dyck words of length 6
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.
Re-interpreting the symbol X as an open parenthesis and Y as a close parenthesis, Cn counts the number of expressions containing n pairs of parentheses which are correctly matched
((())) ()(()) ()()() (())() (()())
Cn is the number of different ways n + 1 factors can be completely parenthesized (or the number of ways of associating n applications of a binary operator). For n = 3, for example, we have the following five different parenthesizations of four factors:
((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))
Successive applications of a binary operator can be represented in terms of a full binary tree. (A rooted binary tree is full if every vertex has either two children or no children.) It follows that Cn is the number of full binary trees with n + 1 leaves:
Sample
Input - 6
Output - 1 1 2 5 14 42
Explanation
The first Catalan numbers for n = 0, 1, 2, 3,4,5,6,7,8,9,10, ... are
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,
Example
#include<iostream>
using namespace std;
long int catalan( int n) {
if (n <= 1){
return 1;
}
long int result = 0;
for (int i=0; i<n; i++){
result += catalan(i)*catalan(n-i-1);
}
return result;
}
int main(){
for (int i=0; i<6; i++)
cout << catalan(i) << " ";
return 0;
}Output
1 1 2 5 14 42
404 Views
