- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find out the length between two cities in shortcuts in Python
Suppose there are n number of cities and the cities are connected with two types of roads; highways and shortcuts. Now, there is a map and only the highways are present on the map and all the shortcuts are absent. The transport division of the cities wants to launch a transport that connects the cities utilizing the highways and the shortcuts. We know there is a shortcut between the two cities when there is no highway between them. Our task here is to find the minimum distances in terms of shortcuts from a starting city to all other cities.
So, if the input is like
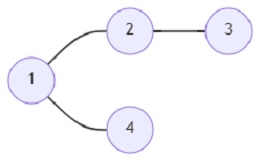
and start vertex (s) is 1, then the output will be 3 1 2.
If we only take shortcuts, the path between cities 1 and 2 will be 1->3->4->2, and the cost will be 3.
Similarly,
1 and 3: 1->3, cost 1.
1 and 4: 1->3->4, cost 2.
To solve this, we will follow these steps −
- graph := a new list containing n sets
- for each pair (x, y) in edges, do
- x := x - 1
- y := y - 1
- insert y into graph[x]
- insert x into graph[y]
- temp_arr := a new array of size n containing value -1
- b_set := a new map containing the key s - 1
- f := a new set containing set difference between numbers 0 to n and b_set
- index := 0
- while size of b_set > 0, do
- for each element a in b_set, do
- temp_arr[a] := index
- nxt := a new map containing values of graph that are not subset of b_set
- f := set difference of f and nxt
- b_set := nxt
- index := index + 1
- for each element a in b_set, do
- return non-zero values of temp_arr
Example
Let us see the following implementation to get better understanding −
def solve(n, edges, s):
graph = [set() for i in range(n)]
for (x, y) in edges:
x -= 1
y -= 1
graph[x].add(y)
graph[y].add(x)
temp_arr = [-1] * n
b_set = {s - 1}
f = set(range(n)).difference(b_set)
index = 0
while len(b_set) > 0:
for a in b_set:
temp_arr[a] = index
nxt = {f for f in f if not b_set.issubset(graph[f])}
f = f.difference(nxt)
b_set = nxt
index += 1
return (' '.join(str(t) for t in temp_arr if t > 0))
print(solve(4, [(1, 2), (2, 3), (1, 4)], 1))
Input
4, [(1, 2), (2, 3), (1, 4)], 1
Output
3 1 2
379 Views
