Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find best position for a service center in Python
Suppose we have a list of positions, which is containing a list of coordinate points where some houses are located. If you want to make a service center at (xc, yc) such that the sum of Euclidean distance from any given point to (xc, yc) is minimum. So we have to find the sum of minimum distance.
So, if the input is like positions = [(10,11),(11,10),(11,12),(12,11)], then the output will be 4.0
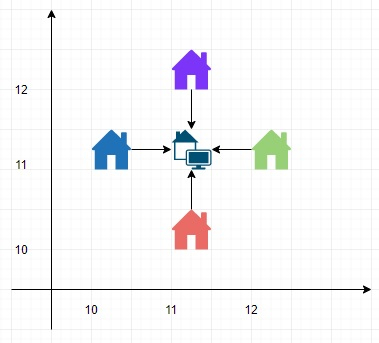
To solve this, we will follow these steps −
numIter := 50
Define a function total() . This will take cx, cy, positions
total := 0.0
for each p in positions, do
x, y := p
total := total + Euclidean distance between (cx, cy) and (x, y)
return total
Define a function fy() . This will take x, positions
l := 0, r := 101
res := 0
for i in range 0 to numIter, do
y1 := l + (r - l) / 3
y2 := r - (r - l) / 3
t1 := total(x, y1, positions)
t2 := total(x, y2, positions)
res := minimum of t1 and t2
if t1 < t2, then
r := y2
otherwise,
l := y1
return res
Define a function fx() . This will take positions
l := 0, r := 101
res := 0
for i in range 0 to numIter, do
x1 := l + (r - l) / 3
x2 := r - (r - l) / 3
t1 := fy(x1, positions)
t2 := fy(x2, positions)
res := minimum of t1 and t2
if t1 < t2, then
r := x2
otherwise,
l := x1
return res
From the main method, return fx(positions)
Example
Let us see the following implementation to get better understanding
from math import sqrt
def solve(points):
numIter = 50
def total(cx, cy, positions):
total = 0.0
for p in positions:
x, y = p
total += sqrt((cx - x) * (cx - x) + (cy - y) * (cy - y))
return total
def fy(x, positions):
l, r = 0, 101
res = 0
for i in range(numIter):
y1 = l + (r - l) / 3
y2 = r - (r - l) / 3
t1 = total(x, y1, positions)
t2 = total(x, y2, positions)
res = min(t1, t2)
if t1 < t2:
r = y2
else:
l = y1
return res
def fx(positions):
l, r = 0, 101
res = 0
for i in range(numIter):
x1 = l + (r - l) / 3
x2 = r - (r - l) / 3
t1 = fy(x1, positions)
t2 = fy(x2, positions)
res = min(t1, t2)
if t1 < t2:
r = x2
else:
l = x1
return res
return fx(positions)
positions = [(10,11),(11,10),(11,12),(12,11)]
print(solve(positions))Input
[(10,11),(11,10),(11,12),(12,11)]
Output
4.0
79 Views
