Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print Binary Tree in 2-Dimensions in C++
In this problem, we are given a binary tree and we have to print it two dimensional plane.
Binary Tree is a special tree whose every node has at max two child nodes. So, every node is either a leaf node or has one or two child nodes.
Example,
Let’s take an example to understand the topic better −
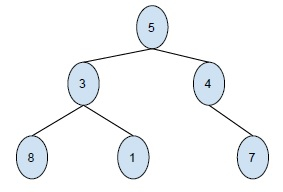
Output -
7 4 5 1 3 8
Now as we have seen in the example, the nodes of the tree are printed in a 2-D output screen horizontally.
Here, we have flipped the tree by 90o.
Let’s see what the new horizontal tree is made up of,
The tree data structure is stored in a horizontal way which includes
The root at the 1st position in horizontal view n lines below the starting line. i.e. root will be at the start of the nth line.
The new levels of the tree are in lines n+i and n-i. And at i tab spaces away from the start of the line.
And the rightmost leaf node of the tree is printed in the first line. Whereas the leftmost node of the tree is printed at the last line.
Example
Let’s create a program based on this logic −
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
#define COUNT 10
class Node{
public:
int data;
Node* left, *right;
Node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
void printTree(Node *root, int space){
if (root == NULL)
return;
space += COUNT;
printTree(root->right, space);
for (int i = COUNT; i < space; i++)
cout<<"\t";
cout<<root->data<<"\n";
printTree(root->left, space);
}
int main(){
Node *root = new Node(43);
root->left = new Node(25);
root->right = new Node(67);
root->left->left = new Node(14);
root->left->right = new Node(51);
root->right->left = new Node(26);
root->right->right = new Node(97);
root->left->left->left = new Node(81);
root->left->left->right = new Node(49);
root->left->right->left = new Node(07);
root->left->right->right = new Node(31);
root->right->left->left = new Node(29);
root->right->left->right = new Node(13);
root->right->right->left = new Node(59);
root->right->right->right = new Node(16);
printTree(root, 0);
return 0;
}Output
16 97 59 67 13 26 29 43 31 51 7 25 49 14 81
773 Views
