Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Preorder predecessor of a Node in Binary Tree in C++
In this problem, we are given a binary tree and a node value. Our task is to print the preorder predecessor of the node.
Binary Tree is a special type of tree in which each root node can have maximum 2 child nodes.
Preorder Traversal is a way to traverse nodes of the tree. In this we will first traverse root node then left child and then the right child.
Preorder predecessor node is the node that comes before the node in the preorder traversal of the node.
Let’s take an example to understand the problem
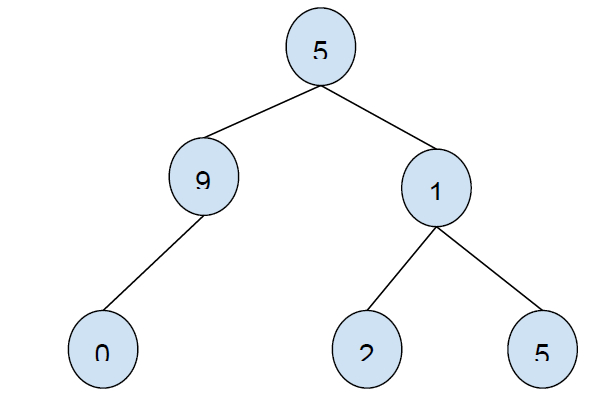
Input: 1 Output: 9
To solve this problem, a navie approach will be to find the preorder traversal of the binary tree and then print the element that comes after the given number.
A more effective solution will involve checking the position of the given number and then searching for its predecessor based on positions. If the node is the root node, then return NULL, no predecessor. If the node is the right child, then the left child will be the predecessor.
Program to show the implementation of the solution
Example
#include <iostream>
using namespace std;
struct Node {
struct Node *left, *right, *parent;
int key;
};
struct Node* insertNode(int key){
Node* temp = new Node;
temp->left = temp->right = temp->parent = NULL;
temp->key = key;
return temp;
}
Node* preOrderPredecessorNode(Node* root, Node* n){
if (n == root)
return NULL;
Node* parent = n->parent;
if (parent->left == NULL || parent->left == n)
return parent;
Node* curr = parent->left;
while (curr->right != NULL)
curr = curr->right;
return curr;
}
int main() {
Node* root = insertNode(99);
root->parent = NULL;
root->left = insertNode(4);
root->left->parent = root;
root->left->left = insertNode(18);
root->left->left->parent = root->left;
root->left->right = insertNode(50);
root->left->right->parent = root->left;
root->right = insertNode(26);
root->right->parent = root;
root->right->left = insertNode(5);
root->right->left->parent = root->right;
root->right->right = insertNode(10);
root->right->right->parent = root->right;
Node* preOrderPredecessor = preOrderPredecessorNode(root, root->left->right);
if (preOrderPredecessor)
cout<<"Preorder Predecessor of "<<root->left->right->key<<" is "<<preOrderPredecessor->key;
else
cout<<"Preorder Predecessor of "<<root->left->right->key<<" is NULL";
return 0;
}Output
Preorder Predecessor of 50 is 18
291 Views
To Continue Learning Please Login