Physics - Spherical Lenses

Introduction

A transparent material (normally glass) bound by two surfaces, of which one or both surfaces are spherical, is known as "spherical lens."

A lens may have two spherical surfaces, bulging outwards (as shown in the image given below), is known as convex lens or a double convex lens.

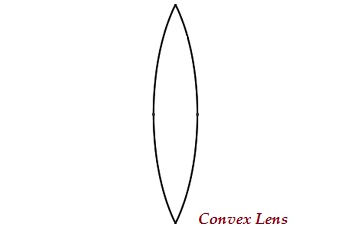
The middle part of this lens is bulged (thicker) and at the both ends, it is narrow.
Convex lens converges the light rays; therefore, it is also known as converging lens.

A lens may have two spherical surfaces, curved inwards (as shown in the image given below), is known as concave lens or a double concave lens.

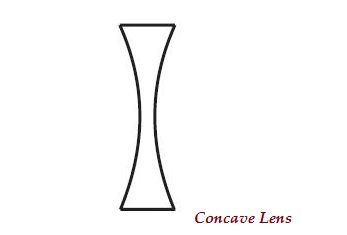
The middle part of this lens is narrow (curved inwards) and the both the edges are thicker.
Concave lens diverges the light rays; therefore, it is also known as diverging lens.
A lens, either a concave or a convex, has two spherical surfaces and each of these surfaces forms a part of the sphere. The centers of these spheres are known as centers of curvature, represented by English letter ‘C.’
As there are two centers of curvature, therefore, represented as ‘C₁’ and ‘C₂.’
An imaginary straight line, passing through both the centers of curvature of a lens, is known as principal axis.
Optical center is the central point of a lens. It is represented by ‘O.’
An aperture is the actual diameter of the circular outline of a spherical lens.
Principal focus of lens is represented by ‘F.’
A lens has usually two foci represented as F₁ and F₂.
Focal length is the distance between the principal focus and the optical center of a lens. It is represented by ‘f.’
The following table illustrates, the nature and position of images formed by a convex lens −

Position of Object	Position of Image	Size of Image	Nature of Image
At infinity	At the focus F₂	Highly diminished, pointsized	Real and inverted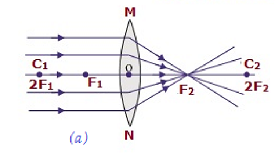
Beyond 2F₁	B/w F₂ and 2F₂	Diminished	Real and inverted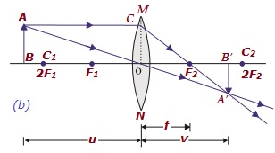
At 2F₁	At 2F₂	Same size	Real and inverted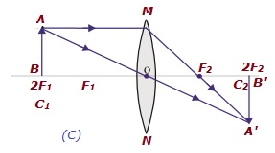
B/w F₁ & 2F₁	Beyond 2F₂	Enlarged	Real and inverted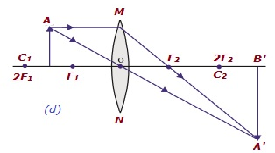
At focus F₁	At infinity	Infinitely large or highly enlarged	Real & inverte d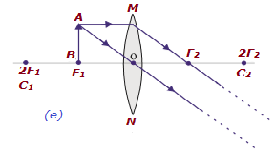
B/w focus F₁ & optical center O	On the same side of the lens as the object	Enlarged	Virtual and erect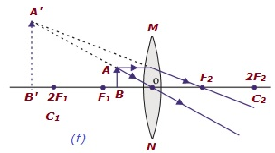

The following table illustrates, the nature and position of images formed by a concave lens −

Position of Object	Position of Image	Relative Size of Image	Nature of Image	Image
At infinity	At the focus F₁	Highly diminishe d, pointsized	Virtual and erect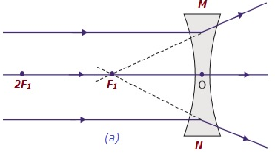
B/w infinity & optical center O of the lens	B/w F₁ & optical center O	Diminishe d	Virtual and erect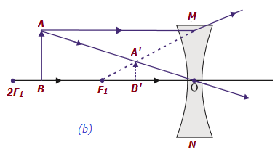

$$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$

Lens formula expresses the relationships among the object-distance (i.e. u), image-distance (i.e. v), and focal length (i.e. f) of a lens.