Physics - Gravitation

---

---

Introduction

• All celestial bodies those found in the universe attract each other and the force of attraction among these bodies is called as the gravitational force.

Universal Law of Gravitation

• Every object in the universe has the property to attract every other object with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them (see the image given below).

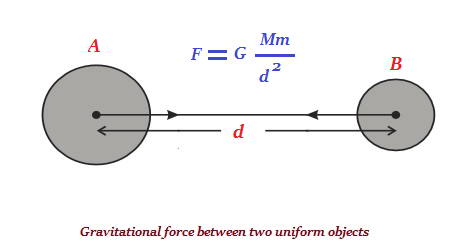
• F = force of attraction between two the objects ‘A’ & ‘B’

• M = mass of ‘A’

• m = mass of ‘B’

• d² = the square of the distance between ‘A’ & ‘B’

• G = is the constant of proportionality and is known as the universal gravitation constant.

• The SI unit of G is N m² kg^–2. It is obtained by substituting the units of force, distance and mass (as given in the following equation −

$$G = \frac{Fd^2}{M \times m}$$

• Henry Cavendish had calculated the value of ‘G’ as 6.673 × 10^–11 N m² kg^–2.

• Henry Cavendish had used a sensitive balance to find the value of ‘G.’

Significance of Universal Law of Gravitation

• Following are the salient significance of the Universal Law of Gravitation −

  • It explains the force that binds all objects (including human beings) to the earth

  • It describes the motion of the moon around the earth

  • It explains the motion of planets around the Sun

  • It clarifies the tides due to the moon and the Sun

Free Fall

• Whenever an object falls towards the earth, it involves an acceleration; this acceleration is produces due to the earth’s gravitational force.

• The acceleration, produces due to the earth’s gravitational force, is known as the acceleration due to the gravitational force of the earth (or acceleration due to gravity).

• The acceleration produces due to the gravitational force is denoted by g.

• As the radius of the earth increases towards the equator (from the poles) the value of ‘g’ becomes greater at the poles than at the equator.

The Value of g

• Value of g is calculated as −

$$g = G\frac{M}{R^2}$$

• G = universal gravitational constant, which is = 6.7 × 10^–11 N m² kg^-2

• M = mass of the earth, which is = 6 × 10²⁴ kg

• R = radius of the earth, which is = 6.4 × 10⁶ m

• So,

$$g = \frac{6.7 \: \times 10^{-11} \: Nm^2 \: kg^{-2} \: \times \: 6 \: \times 10^{24} \: kg}{(6.4 \: \times 10^6 \: m)^2}$$

$=9.8 \: m \: s^{-2}$

• So, the value of acceleration due to gravity of the earth (g) is 9.8 m s^-2.