Images Formed by Spherical Mirrors

Introduction

  • Drawing the ray diagrams is an ideal way to illustrate the formation of images by spherical mirrors.

  • The intersection of at least two reflected rays give the correct position of image of the point object.

  • The following table illustrates the image formed by a concave mirror for different positions of the given object −

Position of Object Position of Image Size of Image Nature of Image Image
At infinity At the focus F Highly diminished, pointsized Real and inverted 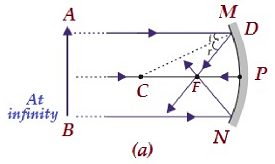At infinity
Beyond C B/w F and C Diminished Real and inverted 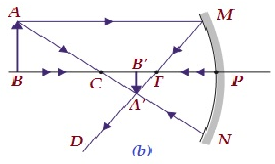Beyond C
At C At C Same size Real and inverted 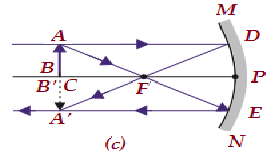At C
B/w C and F Beyond C Enlarged Real and inverted 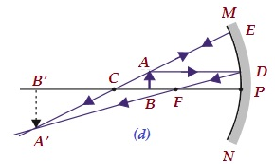B/w C and F
At F At infinity Highly enlarge Real and inverted 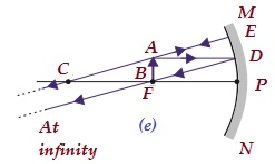At F
B/w P and F Behind the mirror Enlarged Virtual and erect 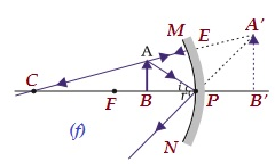B/w P and F

Uses of Concave Mirror

  • In order to get powerful parallel beams of light, concave mirrors are universally used in torches, search-lights, and vehicles headlights.

  • Concave mirror is also used in barber’s saloon, as it gives larger view.

  • Concave mirror is also used by dentists, to see the large images of the teeth of patients.

  • Large concave mirrors are used to concentrate sunlight to produce maximum heat in the solar furnaces.

Image formation by a Convex Mirror

  • The following table illustrates the image formed by a concave mirror for different positions of the given object −

Position of Object Position of Image Size of Image Nature of Image Image
At infinity At the focus F, behind the mirror Highly diminishe d, point sized Virtual and erect 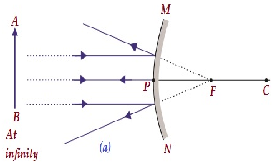At Focus
B/w infinity and pole of the mirror B/w P and F, behind the mirror Diminishe d Virtual and erect 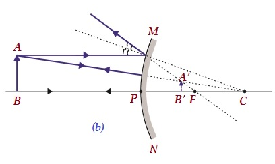B/w infinity

Uses of Convex Mirrors

  • In all vehicles, convex mirrors are universally used as rear-view (wing) mirrors.

  • In vehicles, convex mirrors are preferred, as they give though diminished, but an erect image.

Mirror Formula

  • The formula is expressed as:

    • $$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$$

  • Mirror formula expresses the relationships among the object-distance (i.e. u), image-distance (i.e. v), and focal length (i.e. f) of a spherical mirror.

Advertisements