Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
In $\triangle ABC$, $P$ divides the side $AB$ such that $AP:PB=1:2$. $Q$ is a point in $AC$ such that $PQ \parallel BC$. Find the ratio of the areas of $ \Delta A P Q $ and trapezium BPQC.
Given:
In $\triangle ABC$, $P$ divides the side $AB$ such that $AP:PB=1:2$. $Q$ is a point in $AC$ such that $PQ \parallel BC$.
To do:
We have to find the ratio of the areas of \( \Delta A P Q \) and trapezium BPQC.
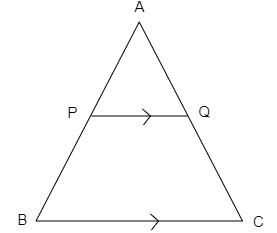
Solution:
In $\triangle APQ$ and $\triangle ABC$,
$\angle PAQ=\angle BAC$ (Common angle)
$\angle APQ=\angle ABC$ (Corresponding angles)
Therefore,
$\triangle APQ \sim\ \triangle ABC$ (By AA similarity)
We know that,
If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.
This implies,
$\frac{ar(\triangle APQ)}{ar(\triangle ABC)}=\frac{AP^2}{AB^2}$
$=\frac{AB^2}{(AP+BP)^2}$
$=\frac{1^2}{(1+2)^2}$
$=\frac{1}{9}$
Therefore,
$\frac{ar(\triangle APQ)}{ar(trapezium\ BPQC)+ar(\triangle APQ)}=\frac{1}{9}$
$9(ar(\triangle APQ))=1(ar(trapezium\ BPQC)+ar(\triangle APQ))$
$(9-1)(ar(\triangle APQ))=ar(trapezium\ BPQC)$
$\frac{ar(\triangle APQ)}{ar(trapezium\ BPQC)}=\frac{1}{8}$
Therefore, the ratio of the areas of \( \Delta A P Q \) and trapezium BPQC is $1:8$.
48 Views
