If $ d_{1}, d_{2}\left(d_{2}>d_{1}\right) $ be the diameters of two concentric circles and $ c $ be the length of a chord of a circle which is tangent to the other circle, prove that $ d_{2}^{2}=c^{2}+d_{1}^{2} $.

Given:

\( d_{1}, d_{2}\left(d_{2}>d_{1}\right) \) are the diameters of two concentric circles and \( c \) are the length of a chord of a circle which is tangent to the other circle.

To do:

We have to prove that \( d_{2}^{2}=c^{2}+d_{1}^{2} \).

Solution:

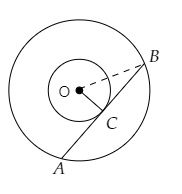
Let $AB$ be a chord of the circle which touches the other circle at $C$.

This implies,

$\triangle OCB$ is a right angled triangle.
By Pythagoras theorem,

$OC^2+CB^2=OB^2$

$(\frac{1}{2} d_{1})^{2}+(\frac{1}{2} c)^{2}=(\frac{1}{2} d_{2})^{2}$   ($C$ bisects $AB$)

Therefore,

$d_{2}^{2}=c^{2}+d_{1}^{2}$

Hence proved.

Tutorialspoint

Updated on: 10-Oct-2022

9 Views

Kickstart Your Career

Get certified by completing the course

Get Started