Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
OpenCV Python – How to find the shortest distance between a point in the image and a contour?
We could compute the shortest distance between a point and a contour on the image using cv2.pointPolygonTest() passing the contour points coordinates and the point coordinate as arguments. Before applying cv2.pointPolygonTest() we need to compute the contours in the image. We could follow the below given steps to find shortest distance between a given point and a contour of an object in an image-
Import the required library. In all the following Python examples, the required Python library is OpenCV. Make sure you have already installed it.
Read an input image using cv2.imread(). The RGB image read using this method is in BGR format. Optionally assign the read BGR image to img.
Now convert this BGR image to grayscale image as below using cv2.cvtColor() function. Optionally assign the converted grayscale image to gray.
Apply thresholding on the grayscale image to convert it to a binary image. Adjust the second parameter (threshValue) for better binary image.
Find the contours in the binary image.
Select the first contour as cnt or loop over all contours.
Compute shortest distance between a point and the selected contour using cv2.pointPolygonTest() function. Pass the required parameters to this function. To compute the shortest distance between point (250,250) and contour cnt, we use the following code snippet:
dist = cv2.pointPolygonTest(cnt,(250,250),True)
Print the computed shortest distance between the point and object contour in the input image.
Draw the point and the detected contour in the image for better visualization.
Let's understand how to find the shortest distance between a given point and a contour of an object in an image with the help of some Python examples.
Example
In this Python program, we took two points (250,250) and (350,250) on the input image. We compute the shortest distance between the point and the contour in the input image. The input image has only one object contour. We also draw the contour and the points on the image for clear understanding.
# import required libraries import cv2 # load the input image img = cv2.imread('four-point-star.png') # convert the input image to grayscale gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # apply thresholding to convert grayscale to binary image ret,thresh = cv2.threshold(gray,150,255,0) # find the contours contours,hierarchy = cv2.findContours(thresh, cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE) print("Number of contours detected:", len(contours)) # select the first contour cnt = contours[0] # find the shortest distance from point[250,250] dist1 = cv2.pointPolygonTest(cnt,(250,250),True) # print the shortest distance between the point 1 and contour detected. print('Shortest distance of Point 1 from contour:', dist1) dist2 = cv2.pointPolygonTest(cnt,(350,250),True) # print the shortest distance between the point 2 and contour detected. print('Shortest distance of Point 2 from contour:', dist2) # draw the point [250,250] on the image cv2.circle(img, (250,250), 4, (0, 0, 255), -1) cv2.putText(img, "Point 1", (255,255), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2) cv2.circle(img, (350,250), 4, (0, 0, 255), -1) cv2.putText(img, "Point 2", (355,255), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2) # draw contour on the input image cv2.drawContours(img, [cnt], -1, (0,255,255), 3) # display the image with drawn extreme points while True: cv2.imshow("Extreme Points", img) if cv2.waitKey(1) & 0xFF == 27: break cv2.destroyAllWindows()
We will use this image as the Input File for this program −
Output
When you run the above program, it will produce the following output −
Number of contours detected: 1 Shortest distance of Point 1 from contour: -17.72004514666935 Shortest distance of Point 2 from contour: 31.622776601683793
And we get the following window showing the contour and the two points −
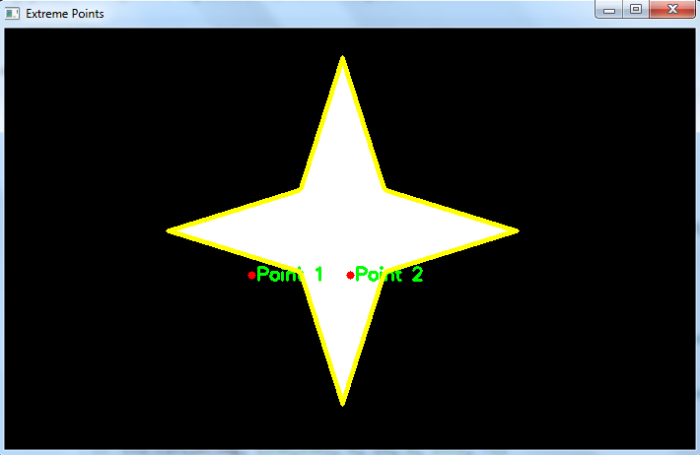
In the above output image, the contours are drawn in yellow color and two points in reed color. The shortest distance between point 1 and contour is negative showing that the point lies outside the contour. And the shortest distance between point 2 and contour is positive showing that the point lies inside the contour. If the shortest distance is zero, it means the point lies on the contour boundary
Example
In this Python program, we took a point (350,250) on the input image. We detect all the object contours in the input image. The image has three contours. We compute the shortest distance between the point and the contours in the input image. We also draw the contours and the point on the image for clear understanding.
# import required libraries import cv2 # load the input image img = cv2.imread('convexhull.png') # convert the input image to grayscale gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # apply thresholding to convert grayscale to binary image ret,thresh = cv2.threshold(gray,100,255,0) # find the contours contours,hierarchy = cv2.findContours(thresh, cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE) print("Number of contours detected:", len(contours)) # draw contour and shape number for i, cnt in enumerate(contours): M = cv2.moments(cnt) x1, y1 = cnt[0,0] img1 = cv2.drawContours(img, [cnt], -1, (0,255,255), 3) cv2.putText(img, f'Contour:{i+1}', (x1, y1), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2) # compute shortest distance of point (350,250) from the contour dist = cv2.pointPolygonTest(cnt,(350,250),True) print(f'Shortest distance of Point (350,250) from contour {i+1}:', dist) cv2.circle(img, (350,250), 4, (0, 0, 255), -1) cv2.imshow("Shapes", img) cv2.waitKey(0) cv2.destroyAllWindows()
We will use this image as the Input File for this program −
Output
When you run the above program, it will produce the following output −
Number of contours detected: 3 Shortest distance of Point (350,250) from contour 1: -83.73768566183328 Shortest distance of Point (350,250) from contour 2: -62.81719509815764 Shortest distance of Point (350,250) from contour 3: -57.27564927611035
And we get the following window showing the contours and the point −
In the above output image, the contours are drawn in yellow color and the point in reed color. Each shortest distance between the point and contours is negative showing that the point lies outside each contour. The absolute distance between the point and contour 3 is minimum in comparison to other distances. Hence the point is closest to the contour 3.
3K+ Views
