Octagon

Introduction

• A polygon is a geometrical figure with a finite number of sides in two-dimension.

• The octagon is an eight-sided polygon.

• An octagon whose all sides are equal is called a regular octagon.

• An octagon has eight interior angles depending upon the side length the interior angles vary between themselves.

• There are different types of octagons depending on the side lengths and interior angles.

• There are a total of twenty diagonals possible in an octagon.

Polygons

• A polygon is a two-dimensional figure made up of connecting a finite number of line segments.

• These line segments are called sides and the number of sides determines the different shapes of polygons.

• A minimum of three sides are required to make a polygon.

• The meeting of two different line segments is called the vertex and at the vertex, the interior angles in a polygon are formed.

• The different measures of angles and sides make different types of polygons like regular, irregular, convex, and concave polygons.

Different shapes of a polygon:

• Triangle is a three-sided polygon

• Quadrilateral is a four-sided polygon

• Pentagon is a five-sided polygon

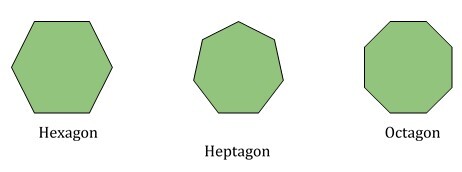
• Hexagon is a six-sided polygon

• Heptagon is a seven-sided polygon

• Octagon is an eight-sided polygon

Similarly, a nine-sided polygon is called a nonagon, and a ten-sided polygon is a decagon.

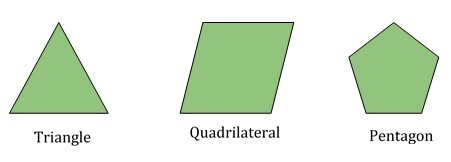
The above three figures represent triangle, quadrilateral, and pentagon.

The below three figures represent hexagon, heptagon, and octagon.

Types of Polygons

• Regular polygon − If a polygon has all its side lengths equal and all its angles are at equal measure then the polygon is a regular polygon.

• Irregular polygon − If a polygon has unequal side lengths and the angles are also not equal then the polygon is irregular.

• Convex polygon − If all the interior angles in a polygon are less than 180 degrees then it is a convex polygon.

• Concave polygon − If at least one of the interior angles in a polygon is more than 180 degrees then it is a concave polygon.

Properties of Polygons

The sum of all the interior angles in a polygon with n sides is equal to $\mathrm{(n-2)\times 180^o}$.

In an n-sided polygon number of diagonals is equal to $\mathrm{\frac{n\times (n-3)}{2}}$

In an n-sided regular polygon each interior angle is equal to $\mathrm{\frac{(n-2)×180^o}{n}}$

In an n-sided regular polygon each exterior angle is equal to $\mathrm{\frac{360^o}{n}}$

Octagons

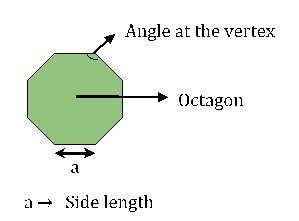
The octagon is an eight-sided polygon. It has eight sides, eight vertices, eight interior angles, and eight exterior angles.

The below diagram is a regular octagon with a side length ‘a’.

The sum of all interior angles in an octagon (n=8) is equal to $\mathrm{(n-2)×180^o=1080^o}$

Types of Octagons

• Regular Octagon − If an octagon has all its side lengths equal and all its angles are at equal measure then the octagon is a regular octagon.

• Irregular octagon − If an octagon has unequal side lengths and the angles are also not equal then the octagon is an irregular octagon.

• Convex Octagon − If all the interior angles in an octagon are less than 180 degrees then it is a convex octagon.

• Concave Octagon − If at least one of the interior angles in an octagon is more than 180 degrees then it is a concave octagon.

Properties of Octagons

• The measure of all interior angles in a regular octagon is: n = 8

  $$\mathrm{\frac{(n-2)×180^o}{n}=\frac{(8-2)×180^o}{8} = 135\: degrees. }$$

• The measure of all exterior angles in a regular octagon is: n = 8

  $$\mathrm{\frac{360^o}{n}=\frac{360^o}{8}= 45\: degrees.}$$

• The number of diagonals in an octagon is: n = 8

  $$\mathrm{\frac{n×(n-3)}{2}=\frac{8×(8-3)}{2}=20}$$

• The perimeter of an octagon is equal to the sum of the lengths of all the sides. In a regular octagon with side length ‘a’ the perimeter is equal to 8a.

• In a regular octagon with side length ‘a’ the area of the regular octagon is equal to $\mathrm{2×a^2×(1+\sqrt{2}).}$

• All regular octagons are convex octagons as all the angles are equal to 135 degrees which is less than 180 degrees whereas an irregular octagon can be both convex or concave octagon.

• By joining any two opposite vertices longest diagonal in an octagon is formed the length of the longest diagonal in a regular octagon with side length ‘a’ is: $\mathrm{a×\sqrt{4+2×\sqrt{2}}}$

Lines of Symmetry of Octagons

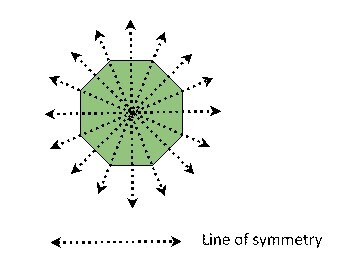
If a line divides the polygon into two halves then it is called line of symmetry. In a regular octagon, there can be eight possible lines of symmetry. In the below figure a regular polygon with eight lines of symmetry.

Octagons in Real life

There are various uses of an octagonal-shaped two-dimensional figure in real life like a traffic board signal with start and stop signs in octagonal shape. There are various analogues wall clocks in octagonal shapes. An umbrella with an upper view is an octagonal shape.

Solved Examples

1) Find the perimeter of an octagon whose side lengths are 2, 3, 4, 5, 6, 7, 8, and 9? All the side lengths are in cm.

The perimeter of an octagon is equal to the sum of its side lengths.

Perimeter = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 44

Perimeter of the octagon is equal to 44cm.

2) Find the area of the octagon if all side lengths are equal to 3cm?

The area of a regular octagon with side length ‘a’ is equal to 2×a²×(1+\sqrt{2})

a = 3; Area =2×a²×(1+\sqrt{2}) =2×3²×(1+\sqrt{2})=43.45

The area of the octagon = 43.45 cm²

3) What is the length of the longest diagonal in a regular polygon of side length equal to 4cm?

The length of the longest diagonal in a regular octagon with side length ‘a’ is: $\mathrm{a×\sqrt{4+2×\sqrt{2}}}$

Given a = 4

The length of the longest diagonal =$\mathrm{a×\sqrt{4+2×\sqrt{2}}=4×\sqrt{4+2×\sqrt{2}}=10.4\: cm }$

The length of the longest diagonal = 10.4cm

Conclusion

In this tutorial, we learned about polygons, types of polygons, some properties of polygons, octagons, properties of octagons, lines of symmetry of octagons, and octagons in real life.

FAQs

1.What is the number of sides a heptagon has?

Heptagon is a seven-sided polygon. So, the heptagon has seven sides.

2.How do we find the number of diagonals in a polygon?

In an n-sided polygon number of diagonals is equal to $\mathrm{\frac{n×(n-3)}{2}}$

3.How many lines of symmetry are possible in a regular octagon?

In a regular octagon, there can be eight possible lines of symmetry.

4.What is the sum of all the interior angles in an octagon?

The sum of all interior angles in an octagon (n=8) is equal to $\mathrm{(n-2)×180^o=1080^o}$

5.What is meant by a convex octagon?

If all the interior angles in an octagon are less than 180 degrees then it is a convex octagon.