Minimum Cost Tree From Leaf Values in Python

Suppose we have an array arr of positive integers, consider all binary trees such that −

• Each node has either 0 or 2 children;
• The values of arr array correspond to the values of each leaf in an inorder traversal of the tree.
• The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree respectively.

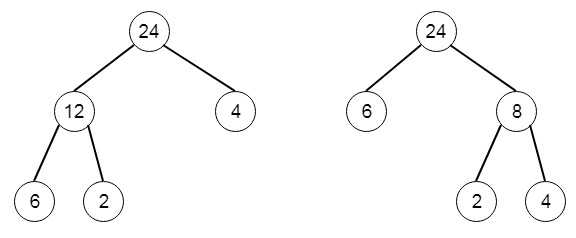
Among all possible binary trees considered, we have to find the smallest possible sum of the values of each non-leaf node. So if the input arr is [6,2,4], then the output will be 32, as there can be possibly two trees −

To solve this, we will follow these steps −

• make a map called memo
• Define a method dp(), this will take i and j as parameters. This will work as follows −
• if j <= i, then return 0
• if (i, j) in the memo, then return memo[(i, j)]
• res := infinity
• for k in range i to j – 1
  • res := min of res, dp(i, k) + dp(k + 1, j) + (max of subarray of arr from index i to k + 1) * max of subarray of arr from k + 1 to j + 1
• memo[(i, j)] := res
• return memo[(i, j)]
• The main method will call this dp() method as − call dp(0, length of arr - 1)

Let us see the following implementation to get better understanding −

Example

class Solution(object):
   def mctFromLeafValues(self, arr):
      """
      :type arr: List[int]
      :rtype: int
      """
      self. memo = {}
      def dp(i,j):
         if j<=i:
            return 0
         if (i,j) in self.memo:
            return self.memo[(i,j)]
         res = float('inf')
         for k in range(i,j):
            res = min(res,dp(i,k) + dp(k+1,j) + (max(arr[i:k+1])*max(arr[k+1:j+1])))
         self.memo[(i,j)]=res
         return self.memo[(i,j)]
      return dp(0,len(arr)-1)

Input

[6,2,4]

Output

32

Arnab Chakraborty

e

Updated on: 05-Mar-2020

331 Views

Kickstart Your Career

Get certified by completing the course

Get Started