Minimum Cost to cut a board into squares in Python

Suppose we have a board of length p and width q; we have to break this board into p*q number of squares such that cost of breaking is as minimum as possible. Cutting cost for each edge will be given.

So, if the input is like X_slice = [3,2,4,2,5], Y_slice = [5,2,3]

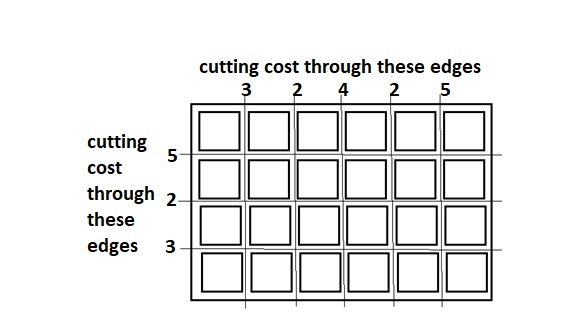
then the output will be 65

To solve this, we will follow these steps −

• res := 0
• horizontal := 1, vertical := 1
• i := 0, j := 0
• while i < m and j < n, do
  • if X_slice[i] > Y_slice[j], then
    • res := res + X_slice[i] * vertical
    • horizontal := horizontal + 1
    • i := i + 1
  • otherwise,
    • res := res + Y_slice[j] * horizontal
    • vertical := vertical + 1
    • j := j + 1
• total := 0
• while i < m, do
  • total := total + X_slice[i]
  • i := i + 1
• res := res + total * vertical
• total := 0
• while j < n, do
  • total := total + Y_slice[j]
  • j := j + 1
• res := res + total * horizontal
• return res

Example

Let us see the following implementation to get better understanding −

 Live Demo

def minCost(X_slice, Y_slice, m, n):
   res = 0
   X_slice.sort(reverse = True)
   Y_slice.sort(reverse = True)
   horizontal = 1
   vertical = 1
   i = 0
   j = 0
   while i < m and j < n:
      if (X_slice[i] > Y_slice[j]):
         res += X_slice[i] * vertical
         horizontal += 1
         i += 1
      else:
         res += Y_slice[j] * horizontal
         vertical += 1
         j += 1
   total = 0
   while (i < m):
      total += X_slice[i]
      i += 1
   res += total * vertical
   total = 0
   while (j < n):
      total += Y_slice[j]
      j += 1
   res += total * horizontal
   return res
m = 6; n = 4
X_slice = [3,2,4,2,5]
Y_slice = [5,2,3]
print(minCost(X_slice, Y_slice, m-1, n-1))

Input

[3,2,4,2,5],[5,2,3]

Output

65

Arnab Chakraborty

Updated on: 27-Aug-2020

115 Views

Kickstart Your Career

Get certified by completing the course

Get Started