Minimize Colors to Paint Graph Such That No Path Has Same Color

Graph coloring is a subset of graph labelling in graph theory. The use of colors stems from coloring the nations on a map, wherein each face is colored. There are several real-world applications for graph coloring, as well as issues of theory. Apart from the traditional forms of problems, other constraints can be imposed on the graph, the manner a color is given, or even the color itself. It has even gained widespread appeal in the shape of the renowned numerical puzzle Sudoku. Graph coloring remains an active area of study.

What Is Vertex Coloring?

The assignment of colors or labels to every vertex or node of any graph such that no two identically colored nodes are linked by an edge is known as vertex coloring. The most popular method of vertex coloring attempts to reduce the number of colors used in an individual graph. This type of coloring is known as minimal vertex coloring.

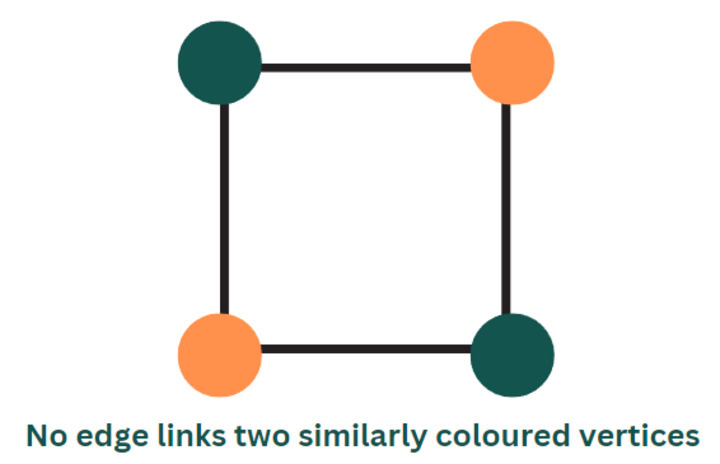
A k-coloring is a vertex coloring of a graph that uses k or lesser colors. A k-colourable graph takes a chromatic number k, and a graph with k chromatic number is mentioned as "k-chromatic graph". The only one-colorable (and hence one-chromatic) graphs are empty, while the two-colourable graphs include bipartite graphs. All of the planar graphs are 4-colorable is stated by the four-color theorem.

Edge Coloring

A graph's edges are appropriately colored when assigned different colors, ensuring no node is next to more than a pair of edges of identical color.  A graph's chromatic index, or edge chromatic number, refers to the minimum number of colors used for edge coloring.

Chromatic Number

The chromatic number is defined as the smallest figure of colours utilized in colouring the vertices or nodes of any graph. The value of this number is usually bigger than one. On the other hand, the chromatic number is one when the graph has a single vertex.

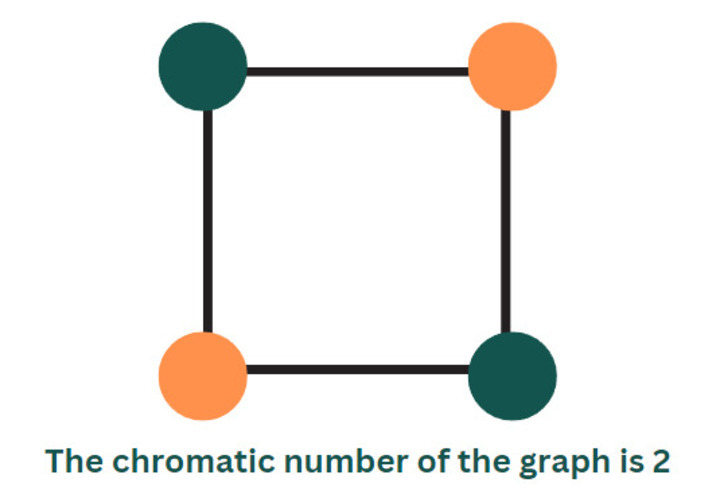
How To Minimalize Colors To Shade A Graph Where No Path Has The Identical Color?

The following is a solution based on the theory of topological sorting −

In "Directed Acyclic Graph (DAG)", topological sorting is defined as the "linear ordering" of the nodes so that, for any directed edge (for example, p, q), the p vertex occurs prior to q in the arrangement.

Topological Sorting is Not Feasible For a Graph if it isn't a DAG

When it comes to topological sorting,

• "Employ a temporary stack."

• "Don't display the vertex immediately; instead, recursively run topological sorting on each of its nearby vertices before pushing it to a stack."

• "Finally, print the stack's contents."

We can see that the lowest number of colors needed equals the length of the graph's longest route.

All nodes with indegree equal to zero can have the same coloring. Eliminate one indegree from their neighbors and cycle over all nodes with indegree = 0.

"If this rule is followed, a particular node will be allocated a colour only after every node above it in all routes has been assigned a color. As a result, this will offer the longest possible length of a path."

To put the idea into action, follow the steps below −

• From the edges provided, construct the adjacency list for a directed graph.

• Keep an in degree vector that holds each node's indegrees.

• Declare a variable (say, depth) to hold a node's depth.

• "During each iteration of topological sorting, a new colour is selected and assigned to minions with indegree 0, and depth is increased by one when a new colour is added."

• As the necessary answer, return the final value of depth.

Example

#include <bits/stdc++.h>
using namespace std;
  
// Function to find minimum number of colours required
int min_colour(int N, int M, vector<int> mat[]){

   // Create an adjacency list
   vector<vector<int> > adj(N + 1);
  
   // Create indeg to store indegree of every minion
   vector<int> indeg(N + 1);
  
   for (int i = 0; i < M; i++) {
  
      // Store mat[i][1] in adj[(mat[i][0])] as mat[i][1] directs to mat[1][0]
      adj[(mat[i][0])].push_back(mat[i][1]);
      indeg[(mat[i][1])]++;
   }

   // Initialize a variable depth to store min different colors required
   int depth = 0;
   queue<int> q;
  
   for (int i = 1; i <= N; i++) {
      if (indeg[i] == 0) {
         q.push(i);
      }
   }
  
   if (q.empty())
      return 0;

   // Loop to use Topological sorting
   while (!q.empty()) {
      int size = q.size();
      for (int k = 0; k < size; k++) {
         int e = q.front();
         q.pop();
  
         for (auto it : adj[e]) {
            indeg[it]--;
            if (indeg[it] == 0) {
               q.push(it);
            }
         }
      }
      depth++;
   }
  
   // Return the minimum number of colours
   return depth;
}

// Driver code
int main(){
   int N = 5, M = 6;
   vector<int> mat[] = { { 1, 3 }, { 2, 3 }, { 3, 4 }, { 1, 4 }, { 2, 5 }, { 3, 5 } };

   // Function Call
   cout << min_colour(N, M, mat);
   return 0;
}

Output

According to the above code Output is −

3

Both auxiliary Space and time Complexity are: O(N + M)

Alternative Techniques To Graph Coloring

Let's look at some solutions to the vertex coloring problem.

• The simplest yet inefficient method is brute force search. A brute force search algorithm includes attempting all potential graph colorings and choosing the one with the fewest colours. While this approach promises to find the best solution, it is computationally costly. Furthermore, this method is only applicable to tiny graphs.

• The second strategy is local search. Local search methods improve an existing answer iteratively through modest local adjustments. A local search technique could switch the colours of two nearby vertices in the instance of the vertex colouring problem. It may also attempt to recolour just one vertex.

• Greedy methods can be used to address the vertex colouring problem. These algorithms are straightforward and effective. They do not, however, always produce the best option.

• The vertex coloring problem can also be expressed as an integer linear program. This method can find precise solutions to problems. However, for large graphs, it may turn out extremely costly.

Application of Vertex Coloring

• It has several uses in various domains, including operations research and computer science. Scheduling, routing, register distribution, and wireless frequency allocation are a few of the most popular uses of the vertex coloring issue.

• We must distribute resources to accessible tasks while avoiding conflicts in the scheduling problem. To overcome this challenge, we may represent each job as a vertex in a graph and every resource as a color. This graph also allows us to calculate the chromatic number. As a result, the chromatic number indicates the bare minimum of resources required to execute all jobs without conflict.

• Network routing issue. Data packets must be routed without conflict via a network of nodes in routing. Furthermore, we may describe this problem using vertex coloring, with each node indicating a single vertex and each path expressing color in the graph.

• Variables in a program must be allocated to registers in a computer's processor using compilers. We may use vertex coloring and chromatic number principles to give the fewest registers to run the program.

• In wireless network communication, the vertex coloring problem can be used to assign wireless channels to devices to reduce interference.

Conclusion

In graph theory, vertex coloring is a subset of graph labelling involving passing on labels to vertex or node labels to reduce the number of colors used in an individual graph. Scheduling, routing, register distribution, and wireless frequency allocation are all applications of vertex coloring in operations research and computer science.