Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum number of squares that can fit in a right angle isosceles triangle in C++
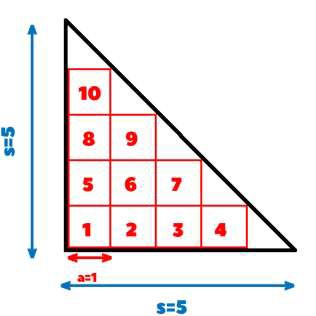
Given the task is to find the maximum number of squares having side ‘a’ that can fit inside a give right angle isosceles triangle with base of ‘s’(An isosceles triangle has at least 2 equal sides).
Let’s now understand what we have to do using an example:
Input
s=5, a=1
Output
10
Explanation − The number of squares in the base can be calculated by dividing s by a and subtracting 1. So the number of squares in base = 5/1 – 1 = 4.
Similarly when the bottom 4 squares are placed then we get a new isosceles triangle with base (s-a) and then we repeat the same procedure and get 3 squares and so on until a single square is placed at the top.
Input
s=7, a=2
Output
3
Approach used in the below program as follows
To find the maximum number of squares we will have to start from the base of the triangle and find out the number of squares.
To find the number of squares we will divide the base s by the side of the square a and subtract 1 from it = s/a – 1.
Then it will leave us another isosceles triangle with base (s - a) which will accommodate one less square than the previous row below it which we can calculate in the following way −
Squares in next row = (s - a)/a – 1 = (s/a – a/a) – 1= s/a - 1 - 1 = s/a – 2 = one square less than the previous row.
The number of squares keep decreasing until it reaches 1, therefore we have to only find the number of squares in the base row and use the formula of adding natural numbers to find the final sum which is −
(n) * (n + 1) / 2
In this case the formula becomes − ((s / a) – 1) * (s / a) / 2
Example
#include<bits/stdc++.h>
using namespace std;
int Max(int s, int a){
//formula for calculating maximum squares
return ((s / a) - 1) * (s / a) / 2;
}
//Main function
int main(){
int s = 5, a = 1;
cout <<"Maximum squares possible are: "<<Max(s,a);
return 0;
}Output
10
227 Views
To Continue Learning Please Login