Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
JavaScript Program for Diagonally Dominant Matrix
Matrix or matrices are great tools in computer science and mathematics for quickly approximating difficult calculations. A matrix is a collection of numbers organized in rows and columns that can represent data or mathematical problems.
By this article, we will learn about the Diagonally Dominant matrix. We will look at the concepts, algorithms, and examples of diagonally dominant matrices, as well as their implementations in a variety of programming languages.
Diagonally Dominant Matrix
We can call a square matrix diagonally dominant if, for every row in the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the non-diagonal entries. In simpler words, if the sum of elements in a matrix other than the diagonal element is less than the diagonal matrix.
If We have a square matrix a with i rows and j columns, we can denote this as a diagonally dominant matrix using a mathematical equation as −
$$\mathrm{|\:a_{ii}\:|\:\geq\:\displaystyle\sum\limits_{jeq\:i}\:|\:a_{ij}|}$$ for all i Where aij denotes the entry in the ith and jth column
Example
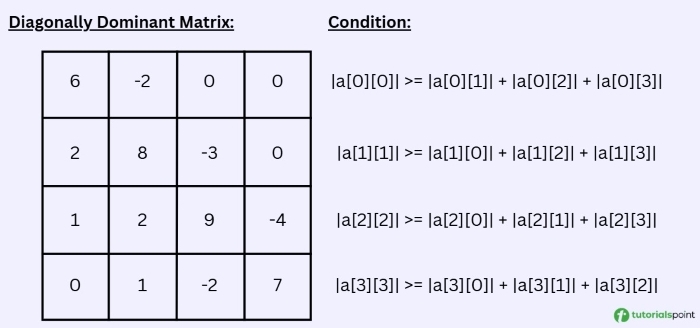
A = [ [6, -2, 0, 0], [2, 8, -3, 0], [1, 2, 9, -4], [0, 1, -2, 7] ]
This matrix is diagonally dominant because it satisfies the following −
|a11| ≥ |a12| + |a13| + |a14| == |+6| ≥ |+2| + |+1| + |+0| |a22| ≥ |a21| + |a23| + |a24| == |+8| ≥ |+2| + |+3| + |+0| |a33| ≥ |a31| + |a32| + |a34| == |+9| ≥ |+1| + |+2| + |+4| |a44| ≥ |a41| + |a42| + |a43| == |+7| ≥ |+0| + |+1| + |+2|
Problem Statement
Given a square matrix, write a JavaScript program to check whether the matrix is diagonally dominant or not.
Example
Let's consider a 3x3 matrix −
| 4 -1 0 | | -1 4 -1| | 0 -1 4 |
Here, the diagonal elements of each row are 4, 4 and 4 respectively, which are greater than the sum of the absolute values of the other elements in that row. Hence, this matrix is diagonally dominant.
Now let’s see the methods to solve the above problem.
Method 1: Brute Force
The brute force method includes iterating over each row of the matrix and determining whether the diagonal element is bigger than the sum of the absolute values of the other elements in that row.
Algorithm
Iterate through the matrix's rows.
Calculate the total of the absolute values of the other components in each row.
Check to see if the row's diagonal element is more than or equal to the sum determined in step 2.
Continue iterating to the next row if the diagonal element is more than or equal to the sum.
Return false if the diagonal element is less than the sum, indicating that the matrix is not diagonally dominating.
Example
<!DOCTYPE html>
<html>
<body>
<div id="matrix"></div>
<div id="output"></div>
<script>
function isDiagonallyDominant(matrix) {
const rows = matrix.length;
const cols = matrix[0].length;
for(let i = 0; i < rows; i++) {
let sum = 0;
for(let j = 0; j < cols; j++) {
if(i !== j) {
sum += Math.abs(matrix[i][j]);
}
}
if(Math.abs(matrix[i][i]) < sum) {
return false;
}
}
return true;
}
const matrix = [[4, -1, 0], [-1, 4, -1], [0, -1, 4]];
const output = isDiagonallyDominant(matrix) ? 'Matrix is diagonally dominant.' : 'Matrix is not diagonally dominant.';
document.getElementById('matrix').innerHTML = 'Matrix: ' + JSON.stringify(matrix);
document.getElementById('output').innerHTML = 'Output: ' + output;
</script>
</body>
</html>
Time Complexity: O(n2), where n is the size of the matrix.
Method 2: Sorting
In this method, we sort the absolute values of each row in descending order. Then we determine whether the diagonal element of that row is bigger than or equal to the sum of the greatest n-1 absolute values, where n is the matrix's size.
Algorithm
Iterate through the matrix's rows.
Sort the absolute values of the row's items in descending order.
Add the biggest n-1 absolute values, where n is the size of the matrix.
Check to see if the row's diagonal element is more than or equal to the sum determined in step 3.
Continue iterating to the next row if the diagonal element is more than or equal to the sum.
Return false if the diagonal element is less than the sum, indicating that the matrix is not diagonally dominating.
Example
<!DOCTYPE html>
<html>
<body>
<h2>Diagonally Dominant Matrix</h2>
<p id="matrix"></p>
<p id="output"></p>
<script>
function isDiagonallyDominant(matrix) {
const rows = matrix.length;
const cols = matrix[0].length;
for(let i = 0; i < rows; i++) {
const sortedRow = matrix[i].map(Math.abs).sort((a, b) => b - a);
const sum = sortedRow.slice(1, cols).reduce((acc, val) => acc + val, 0);
if(sortedRow[0] < sum) {
return false;
}
}
return true;
}
// Example matrix
const matrix = [[4, -1, 0], [-1, 4, -1], [0, -1, 4]];
// Display input matrix
const matrixElement = document.getElementById("matrix");
matrixElement.innerHTML = "Input Matrix: <br>" + JSON.stringify(matrix);
// Check if the matrix is diagonally dominant
const isDominant = isDiagonallyDominant(matrix);
// Display output
const outputElement = document.getElementById("output");
outputElement.innerHTML = "Is diagonally dominant: " + isDominant;
</script>
</body>
</html>
Time Complexity: O(n2 log n), where n is the size of the matrix.
Method 3: Row Scaling
In this method, we first scale each row of the matrix so that its diagonal element equals 1. Then we look to see if the absolute values of the other entries in that row are less than one.
Algorithm
Iterate through the matrix's rows.
Identify the row with the highest absolute value.
Scale the row till the diagonal element equals 1.
Check to see if the absolute values of the remaining entries in that row are less than 1.
Return true if all of the rows satisfy the criterion in step 4, indicating that the matrix is diagonally dominating.
Return false if any row does not satisfy the requirement in step 4, indicating that the matrix is not diagonally dominant.
Example
<!DOCTYPE html>
<html>
<body>
<h3>Diagonally Dominant Matrix</h3>
<p>Matrix:</p>
<pre id="matrix"></pre>
<p>Is diagonally dominant: <span id="output"></span></p>
<script>
function isDiagonallyDominant(matrix) {
const rows = matrix.length;
const cols = matrix[0].length;
for(let i = 0; i < rows; i++) {
const maxAbsVal = Math.max(...matrix[i].map(Math.abs));
if(maxAbsVal === 0) {
return false;
}
const scale = 1 / maxAbsVal;
for(let j = 0; j < cols; j++) {
matrix[i][j] *= scale;
}
const sum = matrix[i].slice(0, i).reduce((acc, val) => acc + Math.abs(val), 0) + matrix[i].slice(i+1, cols).reduce((acc, val) => acc + Math.abs(val), 0);
if(sum >= 1) {
return false;
}
}
return true;
}
const matrix = [[4, -1, 0], [-1, 4, -1], [0, -1, 4]];
document.getElementById('matrix').innerHTML = matrix.map(row => row.join(' ')).join('
');
document.getElementById('output').innerHTML = isDiagonallyDominant(matrix) ? 'true' : 'false';
</script>
</body>
</html>
Time Complexity: O(n3), where n is the size of the matrix.
Conclusion
In this blog we have talked about a program to find if a matrix is diagonally dominant or not by various methods. Some of them are using loop, sorting and row scaling approaches. Hope you found this information useful.
91 Views
