Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How Decibel Operations are Performed Through Logarithms?
Introduction to dB Operations
The ‘decibel’ is a form of representing ratios on a logarithmic scale instead of linear scale. They are used across several disciplines of STEM. In this article, we will see how to perform calculations using decibels with examples pertaining to electrical engineering. We know that the ‘decibel’ represents the ratio of two quantities on the logarithmic scale. While comparing two quantities, one of them will be considered as a reference. This article discusses the basic operations that could be performed on decibels with some examples.
Basic operations based on logarithms
Logarithmic Multiplication
The logarithm of the product of two numbers taken on a linear scale is equal to the sum of the two numbers in their logarithmic forms.
We know that multiplication on a linear scale is equivalent to addition on a logarithmic scale.
(A×B)dB=(A)dB + (B)dB
Where,
A(dB)=10log10A
Let us consider a cascaded three amplifier system where the gains of the first, second, and third amplifiers are 10, 15 and 20, respectively. The input power of the signal fed to the first amplifier is 5 W.
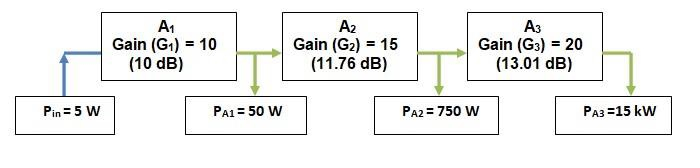
The overall gain of the system is the ratio of PA3 / Pin
The overall linear gain of the system is the product of the linear gains of individual amplifiers. This gives us overall linear gain AP to be
$$A_{p}=\frac{P_{A3}}{P_{in}}=G_{1}G_{2}G_{3}=3000$$
$$P_{A3}=A_{P}P_{in}=15kW$$
The overall ‘dB’ power gain is given as
10 log103000=34.77dB
We also know that the overall gain of the system is the sum of individual ‘dB’ gains of the amplifier. Since we are dealing with power ratios,
$$10log_{10}(A\times\:B\times\:C)=10log_{10}A +10log_{10}B+10log_{10}C$$
$$10log_{10}(10\times\:15\times\:20)=10log_{10}10 +10log_{10}15+10log_{10}20$$
$$=10dB+11.76dB+13.01dB$$
Logarithmic Division
The logarithm of division of two numbers taken on a linear scale is equal to the difference between the two numbers in their logarithmic forms.
$$(A/B)_{dB}=A_{dB}-(B)_{dB}$$
Where
$$A(dB)=10log_{10}A$$
Thus, we have
$$log_{10}10-log_{10}5=log_{10}(\frac{10}{5})=log_{10}2$$
208 Views
