Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find the Number of Quadrilaterals Possible from the Given Points using C++
A quadrilateral forms a polygon with four vertices and four edges in Euclidean plane geometry. The name 4-gon etc. Included in other names of quadrilaterals and sometimes they are also known as a square, display style, etc.
In this article, we will explain the approaches to finding the number of quadrilaterals possible from the given points. In this problem, we need to find out how many possible quadrilaterals are possible to create with the provided four points ( x, y ) in the cartesian plane. So here is the example for the given problem −
Input : A( -2, 8 ), B( -2, 0 ), C( 6, -1 ), D( 0, 8 ) Output : 1 Explanation : One quadrilateral can be formed ( ABCD )
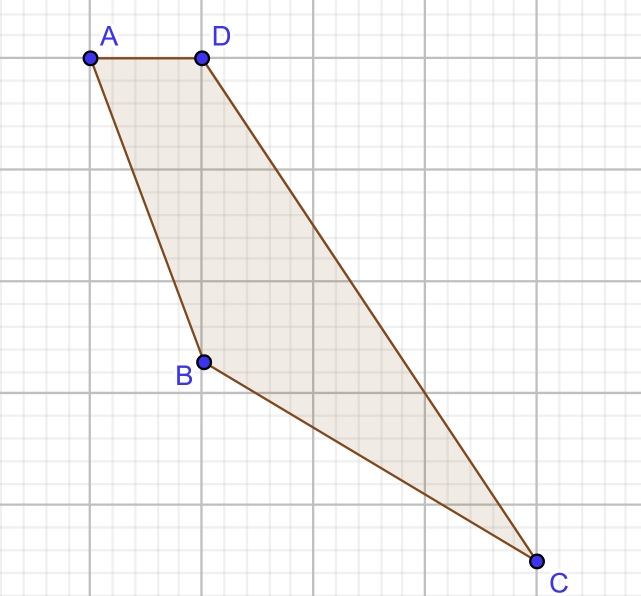
Input : A( 1, 8 ), B( 0, 1 ), C( 4, 0 ), D( 1, 2 ) Output : 3 Explanation : 3 quadrilaterals can be formed (ABCD), (ABDC) and (ADBC).
Approach to Find Solution
We will first check if 3 out of 4 points are collinear and if yes, then no quadrilateral can be formed with the points.
After that, we will check whether any 2 out of 4 points are the same and if yes, then no quadrilateral can be formed.
Now, we will check if the diagonal intersect or not. If yes, then there is only one possible quadrilateral that can be formed, called a convex quadrilateral.
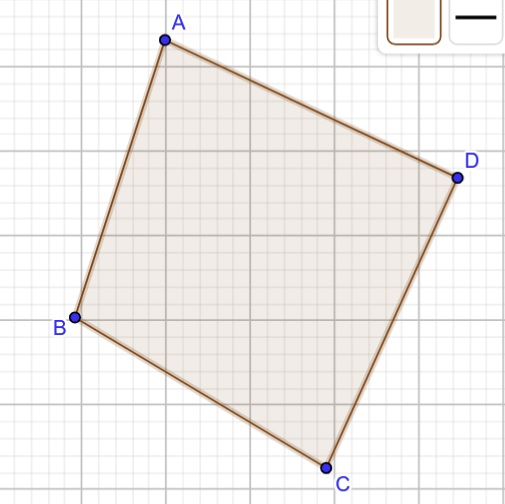
Total number of intersection = 1
If the diagonals do not intersect, three possible quadrilaterals can be formed, called a concave quadrilateral.
Total number of intersection = 0
Example
#include <iostream>
using namespace std;
struct Point{ // points
int x;
int y;
};
int check_orientation(Point i, Point j, Point k){
int val = (j.y - i.y) * (k.x - j.x) - (j.x - i.x) * (k.y - j.y);
if (val == 0)
return 0;
return (val > 0) ? 1 : 2;
}
// checking whether line segments intersect
bool check_Intersect(Point A, Point B, Point C, Point D){
int o1 = check_orientation(A, B, C);
int o2 = check_orientation(A, B, D);
int o3 = check_orientation(C, D, A);
int o4 = check_orientation(C, D, B);
if (o1 != o2 && o3 != o4)
return true;
return false;
}
// checking whether 2 points are same
bool check_similar(Point A, Point B){
// If found similiar then we are returning false that means no quad. can be formed
if (A.x == B.x && A.y == B.y)
return false;
// returning true for not found similiar
return true;
}
// Checking collinearity of three points
bool check_collinear(Point A, Point B, Point C){
int x1 = A.x, y1 = A.y;
int x2 = B.x, y2 = B.y;
int x3 = C.x, y3 = C.y;
if ((y3 - y2) * (x2 - x1) == (y2 - y1) * (x3 - x2))
return false;
else
return true;
}
// main function
int main(){
struct Point A,B,C,D;
A.x = -2, A.y = 8;// A(-2, 8)
B.x = -2, B.y = 0;// B(-2, 0)
C.x = 6, C.y = -1;// C(6, -1)
D.x = 0, D.y = 8;// D(0, 8)
// Checking whether any 3 points are collinear
bool flag = true;
flag = flag & check_collinear(A, B, C);
flag = flag & check_collinear(A, B, D);
flag = flag & check_collinear(A, C, D);
flag = flag & check_collinear(B, C, D);
// If points found collinear
if (flag == false){
cout << "Number of quadrilaterals possible from the given points: 0";
return 0;
}
// Checking if 2 points are same.
bool same = true;
same = same & check_similar(A, B);
same = same & check_similar(A, C);
same = same & check_similar(B, D);
same = same & check_similar(C, D);
same = same & check_similar(A, D);
same = same & check_similar(B, C);
// If similiar point exist
if (same == false){
cout << "Number of quadrilaterals possible from the given points: 0";
return 0;
}
// checking whether diagonal intersect or not
flag = true;
if (check_Intersect(A, B, C, D))
flag = false;
if (check_Intersect(A, C, B, D))
flag = false;
if (check_Intersect(A, B, D, C))
flag = false;
if (flag == true)
cout << "Number of quadrilaterals possible from the given points: 3";
else
cout << "Number of quadrilaterals possible from the given points: 1";
return 0;
}Output
Number of quadrilaterals possible from the given points : 1
Explanation of the Above Code
This code can be understood in the following steps −
Checking whether any three points are collinear and if yes, then the number of a quad. : 0
Checking whether any two points are similar and if yes, then the number of a quad. : 0
Checking whether any line segments intersect:
If yes, then the number of a quad. : 1
If no, then the number of quads. : 3
Conclusion
In this article, we solved finding all possible quadrilaterals that can be formed from the given 4 points. We understand how the number of quadrilaterals depends on collinearity, intersection, and orientation. We also write C++ programs for the same, and we can write this program in any other language like C, Java, and python.
315 Views
