Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count the number of rhombi possible inside a rectangle of given size in C++
We are given a rectangle with dimensions as height X width. The rectangle is represented on a 2D coordinate system with the left-lower corner at point (0,0). So the goal is to count the number of rhombi possible inside this rectangle such that all these conditions are met −
The rhombus has an area more than 0.
The diagonals of the rhombus are parallel to the x and y axis.
The rhombus has integer coordinates for all corners.
Let us understand with examples
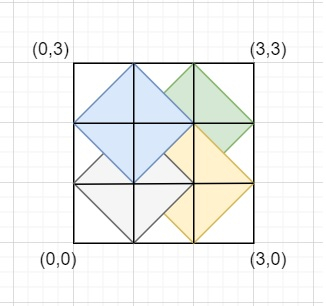
Input − length=3 width=3
Output − Count of number of rhombi possible inside a rectangle of given size are: 4
Explanation − Below figure has a rectangle of height=width=3. Also we can see four rhombi with area >0 and diagonals parallel to both axis (also integer coordinates) −
First [ (1,0), (2,1), (1,2), (0,1) ] Second [ (2,0), (3,1), (2,2), (1,1) ] Third [ (2,1), (3,2), (2,3), (1,2) ] Fourth [ (1,1), (2,1), (1,2), (0,1) ]
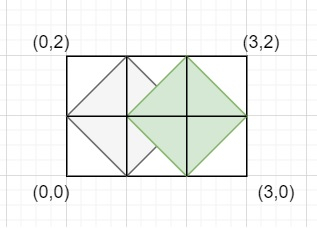
Input − length=2 width=3
Output − Count of number of rhombi possible inside a rectangle of given size are: 2
Explanation − Below figure has a rectangle of height=2 width=3. Also we can see two rhombi inside
The approach used in the below program is as follows
The first rhombus with non zero area and integer coordinates will start from the right upper corner at (2,2). Start traversing from indexes i=j=2 to i<=length and j<=length. Increment i and j by 2 to fix even length (for integer coordinates). The number of rhombi with these diagonals will be (height-i+1)X(width-j+1).
Take length and width as integers.
Function possible_rhombus(int length, int width) takes dimensions of a rectangle and returns the count of rhombi possible inside rectangle which follow all mentioned conditions.
Take the initial count as 0.
Traverse from i=2 to i<=length and j=2 to j<=width.
For each i,j take temp_1=length-i+1 and temp_2=width-j+1
Add temp_1*temp_2 to count.
Increment i and j by 2 (for integer coordinates).
Return count at the end as result.
Example
#include <bits/stdc++.h>
using namespace std;
long long possible_rhombus(int height, int width){
long long count = 0;
for (int i = 2; i <= height; i += 2){
for (int j = 2; j <= width; j += 2){
int temp_1 = height - i + 1;
int temp_2 = width - j + 1;
count += temp_1 * temp_2;
}
}
return count;
}
int main(){
int height = 4, width = 4;
cout<<"Count of number of rhombi possible inside a rectangle of given size are: "<<possible_rhombus(height, width);
return 0;
}Output
If we run the above code it will generate the following output −
Count of number of rhombi possible inside a rectangle of given size are: 16
119 Views
