Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find Corners of Rectangle using mid points in C++
Suppose we have a rectangle ABCD, but we have only the coordinates of the mid points P and Q, and the length of the rectangle L.
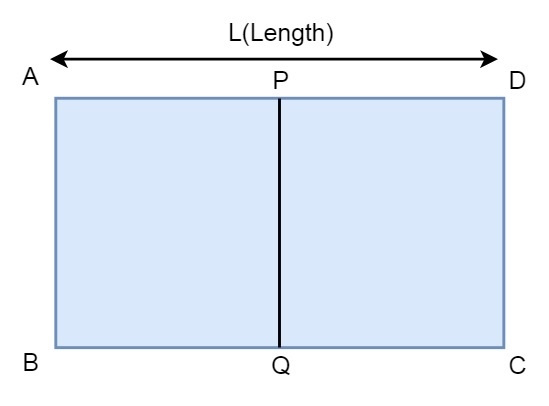
Our task is to find the coordinates of A, B, C and D using the coordinates of P and Q, and the length of side L. For example, if P is (1, 0), and Q is (1, 2), and L is 2, then A, B, C, D will be respectively (0, 0), (0, 2), (2, 2). (2, 0).
There can be three cases that can occur.
- The rectangle is horizontal, so AD and BC are parallel to X axis
- The rectangle is vertical, so AD and BC are parallel to Y axis
- Rectangle is inclined at a certain angle with the axes.
For the third case, we have to find the slope using the coordinates of P and Q. If we get the slope of AD, then we can generate the straight line equation passes through AD, then using the distance formula we will get the result.
$$Slope of AD,m=\frac{px-qx}{py-qy}$$ $$Displacement\:along\:x\:axis, dx=\frac{L}{2\sqrt{1+m^{2}}}$$ $$Displacement\:along\:y\:axis, dy=\frac{mL}{2\sqrt{1+m^{2}}}$$
Example
#include <iostream>
#include <cmath>
using namespace std;
class Point {
public:
float x, y;
Point(float a = 0.0f, float b = 0.0f) {
x = a, y = b;
}
};
void printCorners(Point p, Point q, float l) {
Point a, b, c, d;
if (p.x == q.x) {
a.x = p.x - (l/2.0);
d.x = p.x + (l/2.0);
a.y = d.y = p.y;
b.x = q.x - (l/2.0);
c.x = q.x + (l/2.0);
b.y = c.y = q.y;
}else if (p.y == q.y) {
a.y = p.y - (l/2.0);
d.y = p.y + (l/2.0);
a.x = d.x = p.x;
b.y = q.y - (l/2.0);
c.y = q.y + (l/2.0);
b.x = c.x = q.x;
}else{
float m = (p.x-q.x)/float(q.y-p.y);
float dx = (l /sqrt(1+(m*m))) *0.5 ;
float dy = m*dx;
a.x = p.x - dx;
a.y = p.y - dy;
d.x = p.x + dx;
d.y = p.y + dy;
b.x = q.x - dx;
b.y = q.y - dy;
c.x = q.x + dx;
c.y = q.y + dy;
}
cout << "A (" << a.x << ", " << a.y << ")\n"
<< "B (" << b.x << ", " << b.y << ")\n"
<< "C (" << c.x << ", " << c.y << ")\n"
<< "D (" << d.x << ", " << d.y << ")\n";
}
int main() {
Point p(1, 1), q(-1, -1);
printCorners(p, q, 2*sqrt(2));
}Output
A (0, 2) B (-2, 0) C (0, -2) D (2, 0)
102 Views
