Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find the mid-point of a line in C++
In this problem, we are given two points A and B, starting and ending point of a line. Our task is to create a program to find the mid-point of a line in C++.
Problem Description − Here, we have a line with starting and ending points A(x1, y1) and B(x2, y2). And we need to find the mid-point of the line.
Let’s take an example to understand the problem,
Input
a(x1, y1) = (4, -5) b(x2, y2) = (-2, 6)
Output
(1, 0.5)
Explanation
(x1 + x2)/2 = 4 - 2 / 2 = 1 (y1 + y2)/2 = -5 + 6 / 2 = 0.5
Solution Approach
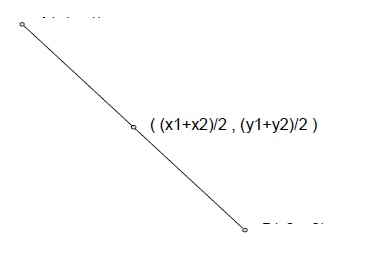
To solve the problem, a simple method is using the geometrical formula for the mid of a line. The formula is given by,
Mid = ( ((x1 + x2)/2), ((y1 + y2)/2) )
Program to illustrate the working of our solution,
Example
#include<iostream>
using namespace std;
int main() {
float point[2][2] = {{-4, 5}, {-2, 6}};
float midX = (float)(( point[0][0] + point[1][0])/2);
float midY = (float)(( point[0][1] + point[1][1])/2);
cout<<"The mid-points are ("<<midX<<" , "<<midY<<")";
return 0;
}Output
The mid-points are (-3 , 5.5)
Updated on: 15-Sep-2020
759 Views
Advertisements