Distance Formula

Introduction

Distance formula used to find the distance measure between two lines .

In an XY-plane or Cartesian plane, the length of a line joining any two coordinates on the plane can be determined by subtracting them.

The coordinates are different depending on their position on the XY plane.

To find the distance between the two points $\mathrm{P(x_{1}\,\:y_{1})\:\&\:Q(x_{2}\,\:y_{2})}$ on the coordinate axis we apply the distance formula. To find the perimeter or the length of the sides of any two-dimensional geometric figures we use the distance formula. The distance formula has a wide range of real-life applications such as navigation of ships, piloting aircraft, the position of satellites, the position of any geometrical locations etc.,

In this tutorial, we will learn about distance formulas in two- dimensional planes and three-dimensional planes with a few solved examples.

Distance Formula in Coordinate Geometry

The distance between the origin and the coordinates on the XY plane are(𝑥1, 𝑦1) & (𝑥2, 𝑦2) where 𝑃 = (𝑥1, 𝑦1) & 𝑄 = (𝑥2, 𝑦2)

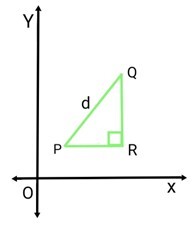
Using the Pythagorean theorem, we can write

$$\mathrm{PQ^{2}\:=\:PR^{2}\:+\:QR^{2}}$$

From the diagram,

$$\mathrm{d^{2}\:=\:(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}$$

By taking the square root on both sides, we get

$$\mathrm{d\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$

This above expression is called the distance formula.

In 2D

If 𝑀(𝑎1, 𝑏1) & 𝑁(𝑎2, 𝑏2) are two points on a given two-dimensional plane or coordinate axis then the distance formula is given by

$$\mathrm{MN\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}}}$$

In 3D

If 𝐴(𝑎1, 𝑏1, 𝑐1 ) & 𝐵(𝑎2, 𝑏2, 𝑐2) are two points on a given three-dimensional plane then the distance formula is given by

$$\mathrm{Ab\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$

Solved Examples

1)Using distance formula find the distance between the two points 𝑷(𝟐, 𝟖) & 𝑸(−𝟒, 𝟏𝟔).

Answer − Given two points $\mathrm{(a_{1}\:,\:b_{1})\:=\:(2,8)\:and\:(a_{2}\:,\:b_{2})\:=\:(-4,16)}$

By using the distance formula,

$$\mathrm{d\:=\:\sqrt{(x_{2}\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{(-4\:2)^{2}\:+\:(16\:-\:8)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{(-6)^{2}\:+\:(8)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{36\:+\:64}}$$

$$\mathrm{PQ\:=\:\sqrt{100}}$$

$$\mathrm{PQ\:=\:10\:metric\:units}$$

Therefore, the distance between the two points 𝑃(2, 8) & 𝑄(−4, 16) is 10.

2)Using distance formula find the distance between the two points 𝑿 (𝟒, −𝟕) & 𝑸 (−𝟐, 𝟏).

Answer −

Given two points $\mathrm{(a_{1}\:,\:b_{1})\:=\:(4,7)\:and\:(a_{2}\:,\:b_{2})\:=\:(-2,1)}$

By using the distance formula,

$$\mathrm{d\:=\:\sqrt{(x_{2}\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$

$$\mathrm{XY\:=\:\sqrt{(-2\:4)^{2}\:+\:(1\:-\:(-7))^{2}}}$$

$$\mathrm{XY\:=\:\sqrt{(-6)^{2}\:+\:(8)^{2}}}$$

$$\mathrm{XY\:=\:\sqrt{36\:+\:64}}$$

$$\mathrm{XY\:=\:\sqrt{100}}$$

$$\mathrm{XY\:=\:10\:metric\:units}$$

Therefore, the distance between the two points𝑋 (4, −7) & 𝑄 (−2, 1) is 10.

3)Find the distance between the two points 𝑴(𝟏, 𝟔) & 𝑵(−𝟐, 𝟑)?

Given two points (𝑎1, 𝑏1) = (1, 6) and (𝑎2, 𝑏2) = (−2, 3)

By using the distance formula,

$$\mathrm{MN\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}}}$$

$$\mathrm{MN\:=\:\sqrt{(-2\:-\:1)^{2}\:+\:(3\:-\:(-6))^{2}}}$$

$$\mathrm{MN\:=\:\sqrt{(-3)^{2}\:+\:(9)^{2}}}$$

$$\mathrm{MN\:=\:\sqrt{9\:+\:81}}$$

$$\mathrm{MN\:=\:\sqrt{90}}$$

$$\mathrm{MN\:=\:9.48683}$$

Therefore, the distance between the two points 𝑀(1, 6) & 𝑁(−2, 3) is 9.48683

4)Using distance formula find the distance between the two points on a threedimensional plane 𝑷(𝟑, 𝟔, 𝟕) & 𝑸(𝟐, 𝟒, 𝟓).

Answer −

Given two points (𝑎1, 𝑏1, 𝑐1 ) = (3, 6, 7) and (𝑎2, 𝑏2, 𝑐2) = (2, 4, 5) on the threedimensional plane

$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{(2\:-\:3)^{2}\:+\:(4\:-\:6)^{2}\:+\:(5\:-\:7)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{(-1)^{2}\:(-2)^{2}\:+\:(-2)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{1\:+\:4\:+\:4}}$$

$$\mathrm{PQ\:=\:\sqrt{9}}$$

$$\mathrm{PQ\:=\:3}$$

Therefore, the distance between the two points 𝑃(3, 6, 7) & 𝑄(2, 4, 5) on a threedimensional plane is 3.

5)Using distance formula find the distance between the two points on a threedimensional plane 𝑷(𝟏, 𝟒, 𝟐) & 𝑸(𝟖, 𝟗, 𝟖)

Answer −

Given two points (𝑎1, 𝑏1, 𝑐1 ) = (1, 4, 2) and (𝑎2, 𝑏2, 𝑐2) = (8, 9, 8) on the threedimensional plane.

$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$

$$\mathrm{PQ\:=\:sqrt{(8\:-\:1)^{2}\:+\:(9\:-\:4)^{2}\:+\:(8\:-\:2)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{(7)^{2}\:+\:(5)^{2}\:+\:(6)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{49\:+\:25\:+\:36}}$$

$$\mathrm{PQ\:=\:\sqrt{110}}$$

$$\mathrm{PQ\:=\:10.48808}$$

Therefore, the distance between the two points 𝑃(1, 4, 2) & 𝑄(8, 9, 8) on a threedimensional plane is 10.48808.

6)Using distance formula find the distance between the two points on a threedimensional plane 𝑨(𝟑, 𝟔, −𝟕) & 𝑩(𝟐, −𝟒, 𝟓).

Answer −

Given two points (𝑎1, 𝑏1, 𝑐1 ) = (3, 6, −7) and (𝑎2, 𝑏2, 𝑐2) = (2, −4, 5) on the threedimensional plane.

$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$

$$\mathrm{PQ\:=\:sqrt{(2\:-\:3)^{2}\:+\:(-4\:-\:6)^{2}\:+\:(5\:+\:7)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{(-1)^{2}\:+\:(-10)^{2}\:+\:(12)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{1\:+\:100\:+\:144}}$$

$$\mathrm{PQ\:=\:\sqrt{245}}$$

$$\mathrm{PQ\:=\:15.6525}$$

Therefore, the distance between the two points 𝑃(3, 6, −7) & 𝑄(2, −4, 5) on a threedimensional plane is 15.6525

7)Find the distance between the two points 𝑰(−𝟏, −𝟏𝟐) & 𝑱(𝟒, 𝟎).

Answer −

Given two points (𝑎1, 𝑏1) = (= 1, −12) and (𝑎2, 𝑏2) = (4, 0)

By using the distance formula,

$$\mathrm{IJ\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}}}$$

$$\mathrm{IJ\:=\:\sqrt{(4\:-\:1)^{2}\:+\:(0\:-\:(-12))^{2}}}$$

$$\mathrm{IJ\:=\:\sqrt{(5)^{2}\:+\:(12)^{2}}}$$

$$\mathrm{IJ\:=\:\sqrt{25\:+\:144}}$$

$$\mathrm{IJ\:=\:\sqrt{169}}$$

$$\mathrm{IJ\:=\:13}$$

Therefore, the distance between the two points 𝑀(1, 6) & 𝑁(−2, 3) is 9.48683

8)Using distance formula find the distance between the two points on a threedimensional plane 𝑷(𝟑, 𝟔, 𝟕) & 𝑸(𝟐, 𝟒, 𝟓).

Answer −

Given two points (𝑎1, 𝑏1, 𝑐1 ) = (3, 6, 7) and (𝑎2, 𝑏2, 𝑐2) = (2, 4, 5) on the threedimensional plane.

$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$

$$\mathrm{PQ\:=\:sqrt{(2\:-\:3)^{2}\:+\:(4\:-\:6)^{2}\:+\:(5\:-\:7)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{(-1)^{2}\:+\:(-2)^{2}\:+\:(-2)^{2}}}$$

$$\mathrm{PQ\:=\:\sqrt{1\:+\:4\:+\:4}}$$

$$\mathrm{PQ\:=\:\sqrt{9}}$$

$$\mathrm{PQ\:=\:3}$$

Therefore, the distance between the two points 𝑃(3, 6, 7) & 𝑄(2, 4, 5) on a threedimensional plane is 3

• The distance formula suggests finding the distance between the given two points or coordinates on a Cartesian plane.

• To find the distance between the two points P(x, y) and Q(x, y) on the coordinate axis we apply the distance formula.

• To find the perimeter or the length of the sides of any two-dimensional geometric figures we use the distance formula.

• The distance formula is in general and for two-dimensional planes is given by

$$\mathrm{d\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$

• The distance formula for a three-dimensional plane is given by

$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$

FAQs

1. Who introduced the coordinate system?

• The coordinate system, also called the Cartesian Plane, is named after the French Mathematician, René Descartes.

• He was the one who introduced the solving method of geometric problems in a coordinate plane.

• He is known as the father of coordinate geometry

2. What are Intercepts?

When a straight line or a curve passes through the coordinate axes of a Cartesian plane, it contacts two points, one on the horizontal axis and another on the vertical axis. These points of contact are called the Intercepts of a plane.

3. What are dihedral angles?

The angle formed when two planes intersect is called the dihedral angle. The planes that intersect are considered to be Cartesian planes.

4. Give some real-life applications of coordinate geometry?

• To ensure flight safety, coordinate geometry is used to update the location of flights.

• It is used to gather information on the position of satellites

• The latitude and longitude of the earth can be described by the coordinate system

• The prediction of the future paths of a storm can be described with the help of coordinate geometry.

• The location of cities and states on a map is positioned with the help of coordinate geometry.

5. What is the difference between Euclidean and Non-Euclidean Geometry?

Euclidean Geometry deals with the study of two-dimensional or flat objects whereas Non-Euclidean geometry deals with the study of curved surfaces.

6. What is a Euclidean vector?

A geometric object which has both magnitude and direction is called a Euclidean vector or simply a vector. It is also called a spatial vector or a geometric vector. This type of vector can be added with other vectors.

7. What is a slope intercept form in coordinate geometry?

When a line crosses the axes, it intersects one or two points in the coordinate graph.

The distance of the unit a from the origin of the graph is where the straight line cuts the y-axis

The general equation of line in point form is $\mathrm{y\:-\:y_{1}\:=\:m(x\:-\:x_{1})}$

The equation of the straight line with slope m crossing the point (0, 𝑎) is given by

$\mathrm{y\:-\:a\:=\:m(x\:-\:0)\:where\:(0,\:a)\:is\:(x_{1}\:-\:y_{1})}$

Therefore $\mathrm{y\:=\:mx\:+\:a}$ is the equation of a line in slope-intercept form.