
- Discrete Mathematics - Home
- Discrete Mathematics Introduction
- Mathematical Statements and Operations
- Atomic and Molecular Statements
- Implications
- Predicates and Quantifiers
- Sets
- Sets and Notations
- Relations
- Operations on Sets
- Venn Diagrams on Sets
- Functions
- Surjection and Bijection Functions
- Image and Inverse-Image
- Mathematical Logic
- Propositional Logic
- Logical Equivalence
- Deductions
- Predicate Logic
- Proof by Contrapositive
- Proof by Contradiction
- Proof by Cases
- Rules of Inference
- Group Theory
- Operators & Postulates
- Group Theory
- Algebric Structure for Groups
- Abelian Group
- Semi Group
- Monoid
- Rings and Subring
- Properties of Rings
- Integral Domain
- Fields
- Counting & Probability
- Counting Theory
- Combinatorics
- Additive and Multiplicative Principles
- Counting with Sets
- Inclusion and Exclusion
- Bit Strings
- Lattice Path
- Binomial Coefficients
- Pascal's Triangle
- Permutations and Combinations
- Pigeonhole Principle
- Probability Theory
- Probability
- Sample Space, Outcomes, Events
- Conditional Probability and Independence
- Random Variables in Probability Theory
- Distribution Functions in Probability Theory
- Variance and Standard Deviation
- Mathematical & Recurrence
- Mathematical Induction
- Formalizing Proofs for Mathematical Induction
- Strong and Weak Induction
- Recurrence Relation
- Linear Recurrence Relations
- Non-Homogeneous Recurrence Relations
- Solving Recurrence Relations
- Master's Theorem
- Generating Functions
- Graph Theory
- Graph & Graph Models
- More on Graphs
- Planar Graphs
- Non-Planar Graphs
- Polyhedra
- Introduction to Trees
- Properties of Trees
- Rooted and Unrooted Trees
- Spanning Trees
- Graph Coloring
- Coloring Theory in General
- Coloring Edges
- Euler Paths and Circuits
- Hamiltonion Path
- Boolean Algebra
- Boolean Expressions & Functions
- Simplification of Boolean Functions
- Advanced Topics
- Number Theory
- Divisibility
- Remainder Classes
- Properties of Congruence
- Solving Linear Diophantine Equation
- Useful Resources
- Quick Guide
- Useful Resources
- Discussion
Simplification Of Boolean Functions
Simplification Using Algebraic Functions
In this approach, one Boolean expression is minimized into an equivalent expression by applying Boolean identities.
Problem 1
Minimize the following Boolean expression using Boolean identities −
$$F (A, B, C) = A'B + BC'+ BC + AB'C'$$
Solution
Given,$F (A, B, C) = A'B + BC'+ BC + AB'C'$
Or,$F (A, B, C) = A'B + (BC'+ BC') + BC+ AB'C'$
[By idempotent law, BC = BC + BC]
Or,$F (A, B, C) = A'B + (BC'+ BC) + (BC'+ AB'C')$
Or,$F (A, B, C) = A'B + B(C'+ C) + C'(B+ AB')$
[By distributive laws]
Or,$F (A, B, C) = A'B + B.1 + C'(B + A)$
[ (C' + C) = 1 and absorption law (B + AB')= (B + A)]
Or,$F (A, B, C) = A'B + B + C'(B + A)$
[ B.1 = B ]
Or,$F (A, B, C) = B(A'+ 1) + C'(B + A)$
Or,$F (A, B, C) = B.1 + C'(B + A)$
[ (A' + 1) = 1 ]
Or,$F (A, B, C) = B + C'(B + A)$
[ As, B.1 = B ]
Or,$F (A, B, C) = B + BC' + AC'$
Or,$F (A, B, C) = B(1 + C') + AC'$
Or,$F (A, B, C) = B.1 + AC'$
[As, (1 + C') = 1]
Or,$F (A, B, C) = B + AC'$
[As, B.1 = B]
So,$F (A, B, C) = B + AC'$is the minimized form.
Problem 2
Minimize the following Boolean expression using Boolean identities −
$$F (A, B, C) = (A + B) (A + C)$$
Solution
Given, $F (A, B, C) = (A + B) (A + C)$
Or, $F (A, B, C) = A.A + A.C + B.A + B.C$ [Applying distributive Rule]
Or, $F (A, B, C) = A + A.C + B.A + B.C$ [Applying Idempotent Law]
Or, $F (A, B, C) = A(1 + C) + B.A + B.C$ [Applying distributive Law]
Or, $F (A, B, C) = A + B.A + B.C$ [Applying dominance Law]
Or, $F (A, B, C) = (A + 1).A + B.C$ [Applying distributive Law]
Or, $F (A, B, C) = 1.A + B.C$ [Applying dominance Law]
Or, $F (A, B, C) = A + B.C$ [Applying dominance Law]
So, $F (A, B, C) = A + BC$ is the minimized form.
Karnaugh Maps
The Karnaugh map (Kmap), introduced by Maurice Karnaughin in 1953, is a grid-like representation of a truth table which is used to simplify boolean algebra expressions. A Karnaugh map has zero and one entries at different positions. It provides grouping together Boolean expressions with common factors and eliminates unwanted variables from the expression. In a K-map, crossing a vertical or horizontal cell boundary is always a change of only one variable.
Example 1
An arbitrary truth table is taken below −
| A | B | A operation B |
|---|---|---|
| 0 | 0 | w |
| 0 | 1 | x |
| 1 | 0 | y |
| 1 | 1 | z |
Now we will make a k-map for the above truth table −
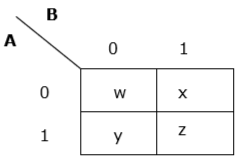
Example 2
Now we will make a K-map for the expression − AB+ AB
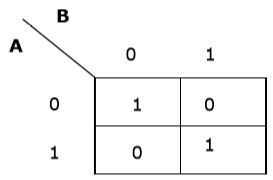
Simplification Using K-map
K-map uses some rules for the simplification of Boolean expressions by combining together adjacent cells into single term. The rules are described below −
Rule 1 − Any cell containing a zero cannot be grouped.
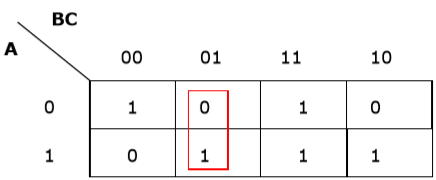
Wrong grouping
Rule 2 − Groups must contain 2n cells (n starting from 1).
Wrong grouping
Rule 3 − Grouping must be horizontal or vertical, but must not be diagonal.
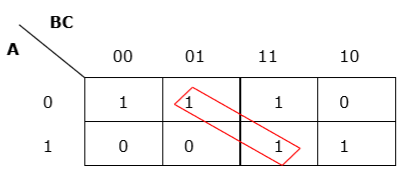
Wrong diagonal grouping
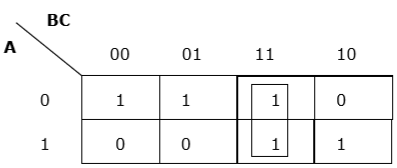
Proper vertical grouping
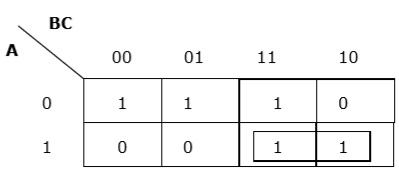
Proper horizontal grouping
Rule 4 − Groups must be covered as largely as possible.
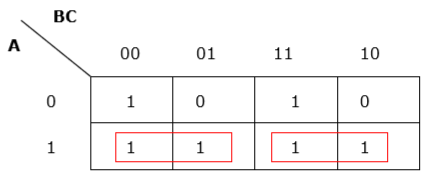
Insufficient grouping
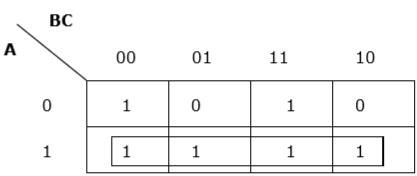
Proper grouping
Rule 5 − If 1 of any cell cannot be grouped with any other cell, it will act as a group itself.
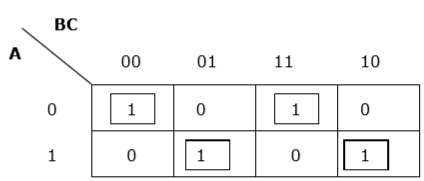
Proper grouping
Rule 6 − Groups may overlap but there should be as few groups as possible.
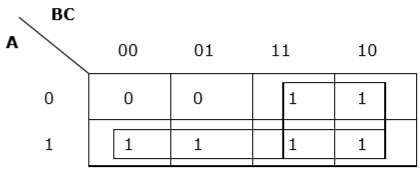
Proper grouping
Rule 7 − The leftmost cell/cells can be grouped with the rightmost cell/cells and the topmost cell/cells can be grouped with the bottommost cell/cells.
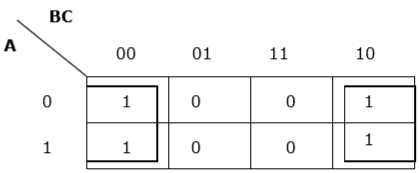
Proper grouping
Problem
Minimize the following Boolean expression using K-map −
$$F (A, B, C) = A'BC + A'BC' + AB'C'+ AB'C$$
Solution
Each term is put into k-map and we get the following −
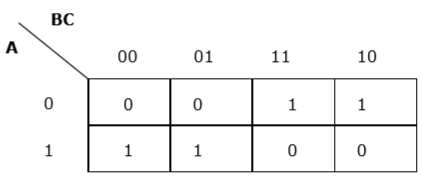
K-map for F (A, B, C)
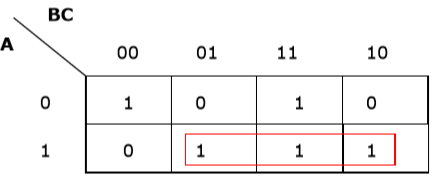
Now we will group the cells of 1 according to the rules stated above −
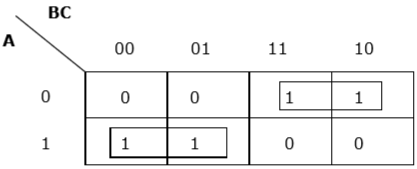
K-map for F (A, B, C)
We have got two groups which are termed as $AB$ and $AB$. Hence, $F (A, B, C) = AB+ AB= A \oplus B$. It is the minimized form.