
- Discrete Mathematics - Home
- Discrete Mathematics Introduction
- Mathematical Statements and Operations
- Atomic and Molecular Statements
- Implications
- Predicates and Quantifiers
- Sets
- Sets and Notations
- Relations
- Operations on Sets
- Venn Diagrams on Sets
- Functions
- Surjection and Bijection Functions
- Image and Inverse-Image
- Mathematical Logic
- Propositional Logic
- Logical Equivalence
- Deductions
- Predicate Logic
- Proof by Contrapositive
- Proof by Contradiction
- Proof by Cases
- Rules of Inference
- Group Theory
- Operators & Postulates
- Group Theory
- Algebric Structure for Groups
- Abelian Group
- Semi Group
- Monoid
- Rings and Subring
- Properties of Rings
- Integral Domain
- Fields
- Counting & Probability
- Counting Theory
- Combinatorics
- Additive and Multiplicative Principles
- Counting with Sets
- Inclusion and Exclusion
- Bit Strings
- Lattice Path
- Binomial Coefficients
- Pascal's Triangle
- Permutations and Combinations
- Pigeonhole Principle
- Probability Theory
- Probability
- Sample Space, Outcomes, Events
- Conditional Probability and Independence
- Random Variables in Probability Theory
- Distribution Functions in Probability Theory
- Variance and Standard Deviation
- Mathematical & Recurrence
- Mathematical Induction
- Formalizing Proofs for Mathematical Induction
- Strong and Weak Induction
- Recurrence Relation
- Linear Recurrence Relations
- Non-Homogeneous Recurrence Relations
- Solving Recurrence Relations
- Master's Theorem
- Generating Functions
- Graph Theory
- Graph & Graph Models
- More on Graphs
- Planar Graphs
- Non-Planar Graphs
- Polyhedra
- Introduction to Trees
- Properties of Trees
- Rooted and Unrooted Trees
- Spanning Trees
- Graph Coloring
- Coloring Theory in General
- Coloring Edges
- Euler Paths and Circuits
- Hamiltonion Path
- Boolean Algebra
- Boolean Expressions & Functions
- Simplification of Boolean Functions
- Advanced Topics
- Number Theory
- Divisibility
- Remainder Classes
- Properties of Congruence
- Solving Linear Diophantine Equation
- Useful Resources
- Quick Guide
- Useful Resources
- Discussion
Discrete Mathematics - Quick Guide
Discrete Mathematics - Introduction
Mathematics can be broadly classified into two categories −
Continuous Mathematics − It is based upon continuous number line or the real numbers. It is characterized by the fact that between any two numbers, there are almost always an infinite set of numbers. For example, a function in continuous mathematics can be plotted in a smooth curve without breaks.
Discrete Mathematics − It involves distinct values; i.e. between any two points, there are a countable number of points. For example, if we have a finite set of objects, the function can be defined as a list of ordered pairs having these objects, and can be presented as a complete list of those pairs.
Topics in Discrete Mathematics
Though there cannot be a definite number of branches of Discrete Mathematics, the following topics are almost always covered in any study regarding this matter −
- Sets, Relations and Functions
- Mathematical Logic
- Group theory
- Counting Theory
- Probability
- Mathematical Induction and Recurrence Relations
- Graph Theory
- Trees
- Boolean Algebra
We will discuss each of these concepts in the subsequent chapters of this tutorial.
Discrete Mathematics - Sets
German mathematician G. Cantor introduced the concept of sets. He had defined a set as a collection of definite and distinguishable objects selected by the means of certain rules or description.
Set theory forms the basis of several other fields of study like counting theory, relations, graph theory and finite state machines. In this chapter, we will cover the different aspects of Set Theory.
Set - Definition
A set is an unordered collection of different elements. A set can be written explicitly by listing its elements using set bracket. If the order of the elements is changed or any element of a set is repeated, it does not make any changes in the set.
Some Example of Sets
- A set of all positive integers
- A set of all the planets in the solar system
- A set of all the states in India
- A set of all the lowercase letters of the alphabet
Representation of a Set
Sets can be represented in two ways −
- Roster or Tabular Form
- Set Builder Notation
Roster or Tabular Form
The set is represented by listing all the elements comprising it. The elements are enclosed within braces and separated by commas.
Example 1 − Set of vowels in English alphabet, $A = \lbrace a,e,i,o,u \rbrace$
Example 2 − Set of odd numbers less than 10, $B = \lbrace 1,3,5,7,9 \rbrace$
Set Builder Notation
The set is defined by specifying a property that elements of the set have in common. The set is described as $A = \lbrace x : p(x) \rbrace$
Example 1 − The set $\lbrace a,e,i,o,u \rbrace$ is written as −
$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$
Example 2 − The set $\lbrace 1,3,5,7,9 \rbrace$ is written as −
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
If an element x is a member of any set S, it is denoted by $x \in S$ and if an element y is not a member of set S, it is denoted by $y \notin S$.
Example − If $S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ but $1.5 \notin S$
Some Important Sets
N − the set of all natural numbers = $\lbrace1, 2, 3, 4, .....\rbrace$
Z − the set of all integers = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z+ − the set of all positive integers
Q − the set of all rational numbers
R − the set of all real numbers
W − the set of all whole numbers
Cardinality of a Set
Cardinality of a set S, denoted by $|S|$, is the number of elements of the set. The number is also referred as the cardinal number. If a set has an infinite number of elements, its cardinality is $\infty$.
Example − $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$
If there are two sets X and Y,
$|X| = |Y|$ denotes two sets X and Y having same cardinality. It occurs when the number of elements in X is exactly equal to the number of elements in Y. In this case, there exists a bijective function f from X to Y.
$|X| \le |Y|$ denotes that set Xs cardinality is less than or equal to set Ys cardinality. It occurs when number of elements in X is less than or equal to that of Y. Here, there exists an injective function f from X to Y.
$|X| \lt |Y|$ denotes that set Xs cardinality is less than set Ys cardinality. It occurs when number of elements in X is less than that of Y. Here, the function f from X to Y is injective function but not bijective.
$If\ |X| \le |Y|$ and $|X| \ge |Y|$ then $|X| = |Y|$. The sets X and Y are commonly referred as equivalent sets.
Types of Sets
Sets can be classified into many types. Some of which are finite, infinite, subset, universal, proper, singleton set, etc.
Finite Set
A set which contains a definite number of elements is called a finite set.
Example − $S = \lbrace x \:| \:x \in N$ and $70 \gt x \gt 50 \rbrace$
Infinite Set
A set which contains infinite number of elements is called an infinite set.
Example − $S = \lbrace x \: | \: x \in N $ and $ x \gt 10 \rbrace$
Subset
A set X is a subset of set Y (Written as $X \subseteq Y$) if every element of X is an element of set Y.
Example 1 − Let, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ and $Y = \lbrace 1, 2 \rbrace$. Here set Y is a subset of set X as all the elements of set Y is in set X. Hence, we can write $Y \subseteq X$.
Example 2 − Let, $X = \lbrace 1, 2, 3 \rbrace$ and $Y = \lbrace 1, 2, 3 \rbrace$. Here set Y is a subset (Not a proper subset) of set X as all the elements of set Y is in set X. Hence, we can write $Y \subseteq X$.
Proper Subset
The term proper subset can be defined as subset of but not equal to. A Set X is a proper subset of set Y (Written as $ X \subset Y $) if every element of X is an element of set Y and $|X| \lt |Y|$.
Example − Let, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ and $Y = \lbrace 1, 2 \rbrace$. Here set $Y \subset X$ since all elements in $Y$ are contained in $X$ too and $X$ has at least one element is more than set $Y$.
Universal Set
It is a collection of all elements in a particular context or application. All the sets in that context or application are essentially subsets of this universal set. Universal sets are represented as $U$.
Example − We may define $U$ as the set of all animals on earth. In this case, set of all mammals is a subset of $U$, set of all fishes is a subset of $U$, set of all insects is a subset of $U$, and so on.
Empty Set or Null Set
An empty set contains no elements. It is denoted by $\emptyset$. As the number of elements in an empty set is finite, empty set is a finite set. The cardinality of empty set or null set is zero.
Example − $S = \lbrace x \:| \: x \in N$ and $7 \lt x \lt 8 \rbrace = \emptyset$
Singleton Set or Unit Set
Singleton set or unit set contains only one element. A singleton set is denoted by $\lbrace s \rbrace$.
Example − $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
Equal Set
If two sets contain the same elements they are said to be equal.
Example − If $A = \lbrace 1, 2, 6 \rbrace$ and $B = \lbrace 6, 1, 2 \rbrace$, they are equal as every element of set A is an element of set B and every element of set B is an element of set A.
Equivalent Set
If the cardinalities of two sets are same, they are called equivalent sets.
Example − If $A = \lbrace 1, 2, 6 \rbrace$ and $B = \lbrace 16, 17, 22 \rbrace$, they are equivalent as cardinality of A is equal to the cardinality of B. i.e. $|A| = |B| = 3$
Overlapping Set
Two sets that have at least one common element are called overlapping sets.
In case of overlapping sets −
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
Example − Let, $A = \lbrace 1, 2, 6 \rbrace$ and $B = \lbrace 6, 12, 42 \rbrace$. There is a common element 6, hence these sets are overlapping sets.
Disjoint Set
Two sets A and B are called disjoint sets if they do not have even one element in common. Therefore, disjoint sets have the following properties −
$n(A \cap B) = \emptyset$
$n(A \cup B) = n(A) + n(B)$
Example − Let, $A = \lbrace 1, 2, 6 \rbrace$ and $B = \lbrace 7, 9, 14 \rbrace$, there is not a single common element, hence these sets are overlapping sets.
Venn Diagrams
Venn diagram, invented in 1880 by John Venn, is a schematic diagram that shows all possible logical relations between different mathematical sets.
Examples
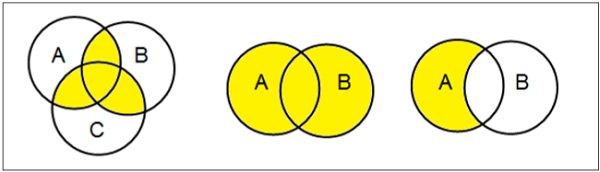
Set Operations
Set Operations include Set Union, Set Intersection, Set Difference, Complement of Set, and Cartesian Product.
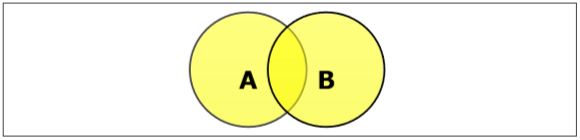
Set Union
The union of sets A and B (denoted by $A \cup B$) is the set of elements which are in A, in B, or in both A and B. Hence, $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$.
Example − If $A = \lbrace 10, 11, 12, 13 \rbrace$ and B = $\lbrace 13, 14, 15 \rbrace$, then $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$. (The common element occurs only once)
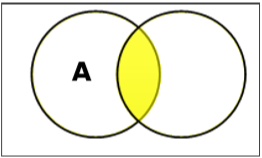
Set Intersection
The intersection of sets A and B (denoted by $A \cap B$) is the set of elements which are in both A and B. Hence, $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$.
Example − If $A = \lbrace 11, 12, 13 \rbrace$ and $B = \lbrace 13, 14, 15 \rbrace$, then $A \cap B = \lbrace 13 \rbrace$.
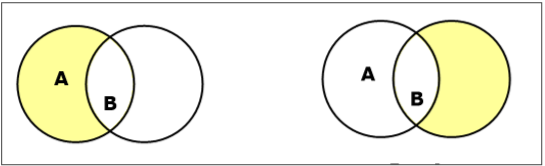
Set Difference/ Relative Complement
The set difference of sets A and B (denoted by $A B$) is the set of elements which are only in A but not in B. Hence, $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$.
Example − If $A = \lbrace 10, 11, 12, 13 \rbrace$ and $B = \lbrace 13, 14, 15 \rbrace$, then $(A - B) = \lbrace 10, 11, 12 \rbrace$ and $(B - A) = \lbrace 14, 15 \rbrace$. Here, we can see $(A - B) \ne (B - A)$
Complement of a Set
The complement of a set A (denoted by $A$) is the set of elements which are not in set A. Hence, $A' = \lbrace x | x \notin A \rbrace$.
More specifically, $A'= (U - A)$ where $U$ is a universal set which contains all objects.
Example − If $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ then $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$
Cartesian Product / Cross Product
The Cartesian product of n number of sets $A_1, A_2, \dots A_n$ denoted as $A_1 \times A_2 \dots \times A_n$ can be defined as all possible ordered pairs $(x_1, x_2, \dots x_n)$ where $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$
Example − If we take two sets $A = \lbrace a, b \rbrace$ and $B = \lbrace 1, 2 \rbrace$,
The Cartesian product of A and B is written as − $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
The Cartesian product of B and A is written as − $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
Power Set
Power set of a set S is the set of all subsets of S including the empty set. The cardinality of a power set of a set S of cardinality n is $2^n$. Power set is denoted as $P(S)$.
Example −
For a set $S = \lbrace a, b, c, d \rbrace$ let us calculate the subsets −
Subsets with 0 elements − $\lbrace \emptyset \rbrace$ (the empty set)
Subsets with 1 element − $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$
Subsets with 2 elements − $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$
Subsets with 3 elements − $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
Subsets with 4 elements − $\lbrace a, b, c, d \rbrace$
Hence, $P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S) | = 2^4 = 16$
Note − The power set of an empty set is also an empty set.
$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
Partitioning of a Set
Partition of a set, say S, is a collection of n disjoint subsets, say $P_1, P_2, \dots P_n$ that satisfies the following three conditions −
-
$P_i$ does not contain the empty set.
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$
-
The union of the subsets must equal the entire original set.
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
-
The intersection of any two distinct sets is empty.
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$
Example
Let $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
One probable partitioning is $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
Another probable partitioning is $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
Bell Numbers
Bell numbers give the count of the number of ways to partition a set. They are denoted by $B_n$ where n is the cardinality of the set.
Example −
Let $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$
The alternate partitions are −
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
Hence $B_3 = 5$
Discrete Mathematics - Relations
Whenever sets are being discussed, the relationship between the elements of the sets is the next thing that comes up. Relations may exist between objects of the same set or between objects of two or more sets.
Definition and Properties
A binary relation R from set x to y (written as $xRy$ or $R(x,y)$) is a subset of the Cartesian product $x \times y$. If the ordered pair of G is reversed, the relation also changes.
Generally an n-ary relation R between sets $A_1, \dots ,\ and\ A_n$ is a subset of the n-ary product $A_1 \times \dots \times A_n$. The minimum cardinality of a relation R is Zero and maximum is $n^2$ in this case.
A binary relation R on a single set A is a subset of $A \times A$.
For two distinct sets, A and B, having cardinalities m and n respectively, the maximum cardinality of a relation R from A to B is mn.
Domain and Range
If there are two sets A and B, and relation R have order pair (x, y), then −
The domain of R, Dom(R), is the set $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$
The range of R, Ran(R), is the set $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$
Examples
Let, $A = \lbrace 1, 2, 9 \rbrace $ and $ B = \lbrace 1, 3, 7 \rbrace$
-
Case 1 − If relation R is 'equal to' then $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom(R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
-
Case 2 − If relation R is 'less than' then $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom(R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
-
Case 3 − If relation R is 'greater than' then $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom(R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
Representation of Relations using Graph
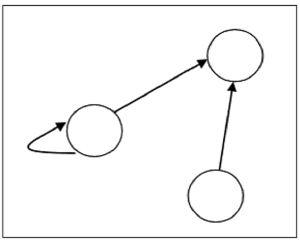
A relation can be represented using a directed graph.
The number of vertices in the graph is equal to the number of elements in the set from which the relation has been defined. For each ordered pair (x, y) in the relation R, there will be a directed edge from the vertex x to vertex y. If there is an ordered pair (x, x), there will be self- loop on vertex x.
Suppose, there is a relation $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ on set $S = \lbrace 1, 2, 3 \rbrace$, it can be represented by the following graph −
Types of Relations
The Empty Relation between sets X and Y, or on E, is the empty set $\emptyset$
The Full Relation between sets X and Y is the set $X \times Y$
The Identity Relation on set X is the set $\lbrace (x, x) | x \in X \rbrace$
-
The Inverse Relation R' of a relation R is defined as − $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
Example − If $R = \lbrace (1, 2), (2, 3) \rbrace$ then $R' $ will be $\lbrace (2, 1), (3, 2) \rbrace$
-
A relation R on set A is called Reflexive if $\forall a \in A$ is related to a (aRa holds)
Example − The relation $R = \lbrace (a, a), (b, b) \rbrace$ on set $X = \lbrace a, b \rbrace$ is reflexive.
-
A relation R on set A is called Irreflexive if no $a \in A$ is related to a (aRa does not hold).
Example − The relation $R = \lbrace (a, b), (b, a) \rbrace$ on set $X = \lbrace a, b \rbrace$ is irreflexive.
-
A relation R on set A is called Symmetric if $xRy$ implies $yRx$, $\forall x \in A$ and $\forall y \in A$.
Example − The relation $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ on set $A = \lbrace 1, 2, 3 \rbrace$ is symmetric.
-
A relation R on set A is called Anti-Symmetric if $xRy$ and $yRx$ implies $x = y \: \forall x \in A$ and $\forall y \in A$.
Example − The relation $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ is anti-symmetric since $x \leq y$ and $y \leq x$ implies $x = y$.
-
A relation R on set A is called Transitive if $xRy$ and $yRz$ implies $xRz, \forall x,y,z \in A$.
Example − The relation $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ on set $A = \lbrace 1, 2, 3 \rbrace$ is transitive.
-
A relation is an Equivalence Relation if it is reflexive, symmetric, and transitive.
Example − The relation $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ on set $A = \lbrace 1, 2, 3 \rbrace$ is an equivalence relation since it is reflexive, symmetric, and transitive.
Discrete Mathematics - Functions
A Function assigns to each element of a set, exactly one element of a related set. Functions find their application in various fields like representation of the computational complexity of algorithms, counting objects, study of sequences and strings, to name a few. The third and final chapter of this part highlights the important aspects of functions.
Function - Definition
A function or mapping (Defined as $f: X \rightarrow Y$) is a relationship from elements of one set X to elements of another set Y (X and Y are non-empty sets). X is called Domain and Y is called Codomain of function f.
Function f is a relation on X and Y such that for each $x \in X$, there exists a unique $y \in Y$ such that $(x,y) \in R$. x is called pre-image and y is called image of function f.
A function can be one to one or many to one but not one to many.
Injective / One-to-one function
A function $f: A \rightarrow B$ is injective or one-to-one function if for every $b \in B$, there exists at most one $a \in A$ such that $f(s) = t$.
This means a function f is injective if $a_1 \ne a_2$ implies $f(a1) \ne f(a2)$.
Example
$f: N \rightarrow N, f(x) = 5x$ is injective.
$f: N \rightarrow N, f(x) = x^2$ is injective.
$f: R\rightarrow R, f(x) = x^2$ is not injective as $(-x)^2 = x^2$
Surjective / Onto function
A function $f: A \rightarrow B$ is surjective (onto) if the image of f equals its range. Equivalently, for every $b \in B$, there exists some $a \in A$ such that $f(a) = b$. This means that for any y in B, there exists some x in A such that $y = f(x)$.
Example
$f : N \rightarrow N, f(x) = x + 2$ is surjective.
$f : R \rightarrow R, f(x) = x^2$ is not surjective since we cannot find a real number whose square is negative.
Bijective / One-to-one Correspondent
A function $f: A \rightarrow B$ is bijective or one-to-one correspondent if and only if f is both injective and surjective.
Problem
Prove that a function $f: R \rightarrow R$ defined by $f(x) = 2x 3$ is a bijective function.
Explanation − We have to prove this function is both injective and surjective.
If $f(x_1) = f(x_2)$, then $2x_1 3 = 2x_2 3 $ and it implies that $x_1 = x_2$.
Hence, f is injective.
Here, $2x 3= y$
So, $x = (y+5)/3$ which belongs to R and $f(x) = y$.
Hence, f is surjective.
Since f is both surjective and injective, we can say f is bijective.
Inverse of a Function
The inverse of a one-to-one corresponding function $f : A \rightarrow B$, is the function $g : B \rightarrow A$, holding the following property −
$f(x) = y \Leftrightarrow g(y) = x$
The function f is called invertible, if its inverse function g exists.
Example
A Function $f : Z \rightarrow Z, f(x)=x+5$, is invertible since it has the inverse function $ g : Z \rightarrow Z, g(x)= x-5$.
A Function $f : Z \rightarrow Z, f(x)=x^2$ is not invertiable since this is not one-to-one as $(-x)^2=x^2$.
Composition of Functions
Two functions $f: A \rightarrow B$ and $g: B \rightarrow C$ can be composed to give a composition $g o f$. This is a function from A to C defined by $(gof)(x) = g(f(x))$
Example
Let $f(x) = x + 2$ and $g(x) = 2x + 1$, find $( f o g)(x)$ and $( g o f)(x)$.
Solution
$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
Hence, $(f o g)(x) \neq (g o f)(x)$
Some Facts about Composition
If f and g are one-to-one then the function $(g o f)$ is also one-to-one.
If f and g are onto then the function $(g o f)$ is also onto.
Composition always holds associative property but does not hold commutative property.
Discrete Mathematics - Propositional Logic
The rules of mathematical logic specify methods of reasoning mathematical statements. Greek philosopher, Aristotle, was the pioneer of logical reasoning. Logical reasoning provides the theoretical base for many areas of mathematics and consequently computer science. It has many practical applications in computer science like design of computing machines, artificial intelligence, definition of data structures for programming languages etc.
Propositional Logic is concerned with statements to which the truth values, true and false, can be assigned. The purpose is to analyze these statements either individually or in a composite manner.
Prepositional Logic Definition
A proposition is a collection of declarative statements that has either a truth value "true or a truth value "false". A propositional consists of propositional variables and connectives. We denote the propositional variables by capital letters (A, B, etc). The connectives connect the propositional variables.
Some examples of Propositions are given below −
- "Man is Mortal", it returns truth value TRUE
- "12 + 9 = 3 2", it returns truth value FALSE
The following is not a Proposition −
"A is less than 2". It is because unless we give a specific value of A, we cannot say whether the statement is true or false.
Connectives
In propositional logic generally we use five connectives which are −
OR ($\lor$)
AND ($\land$)
Negation/ NOT ($\lnot$)
Implication / if-then ($\rightarrow$)
If and only if ($\Leftrightarrow$).
OR ($\lor$) − The OR operation of two propositions A and B (written as $A \lor B$) is true if at least any of the propositional variable A or B is true.
The truth table is as follows −
| A | B | A ∨ B |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| False | False | False |
AND ($\land$) − The AND operation of two propositions A and B (written as $A \land B$) is true if both the propositional variable A and B is true.
The truth table is as follows −
| A | B | A ∧ B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
Negation ($\lnot$) − The negation of a proposition A (written as $\lnot A$) is false when A is true and is true when A is false.
The truth table is as follows −
| A | ¬ A |
|---|---|
| True | False |
| False | True |
Implication / if-then ($\rightarrow$) − An implication $A \rightarrow B$ is the proposition if A, then B. It is false if A is true and B is false. The rest cases are true.
The truth table is as follows −
| A | B | A → B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | True |
| False | False | True |
If and only if ($ \Leftrightarrow $) − $A \Leftrightarrow B$ is bi-conditional logical connective which is true when p and q are same, i.e. both are false or both are true.
The truth table is as follows −
| A | B | A ⇔ B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | True |
Tautologies
A Tautology is a formula which is always true for every value of its propositional variables.
Example − Prove $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ is a tautology
The truth table is as follows −
| A | B | A → B | (A → B) ∧ A | [( A → B ) ∧ A] → B |
|---|---|---|---|---|
| True | True | True | True | True |
| True | False | False | False | True |
| False | True | True | False | True |
| False | False | True | False | True |
As we can see every value of $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ is "True", it is a tautology.
Contradictions
A Contradiction is a formula which is always false for every value of its propositional variables.
Example − Prove $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ is a contradiction
The truth table is as follows −
| A | B | A ∨ B | ¬ A | ¬ B | (¬ A) ∧ ( ¬ B) | (A ∨ B) ∧ [( ¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| True | True | True | False | False | False | False |
| True | False | True | False | True | False | False |
| False | True | True | True | False | False | False |
| False | False | False | True | True | True | False |
As we can see every value of $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ is False, it is a contradiction.
Contingency
A Contingency is a formula which has both some true and some false values for every value of its propositional variables.
Example − Prove $(A \lor B) \land (\lnot A)$ a contingency
The truth table is as follows −
| A | B | A ∨ B | ¬ A | (A ∨ B) ∧ (¬ A) |
|---|---|---|---|---|
| True | True | True | False | False |
| True | False | True | False | False |
| False | True | True | True | True |
| False | False | False | True | False |
As we can see every value of $(A \lor B) \land (\lnot A)$ has both True and False, it is a contingency.
Propositional Equivalences
Two statements X and Y are logically equivalent if any of the following two conditions hold −
The truth tables of each statement have the same truth values.
The bi-conditional statement $X \Leftrightarrow Y$ is a tautology.
Example − Prove $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ are equivalent
Testing by 1st method (Matching truth table)
| A | B | A ∨ B | ¬ (A ∨ B) | ¬ A | ¬ B | [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| True | True | True | False | False | False | False |
| True | False | True | False | False | True | False |
| False | True | True | False | True | False | False |
| False | False | False | True | True | True | True |
Here, we can see the truth values of $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ are same, hence the statements are equivalent.
Testing by 2nd method (Bi-conditionality)
| A | B | ¬ (A ∨ B ) | [(¬ A) ∧ (¬ B)] | [¬ (A ∨ B)] ⇔ [(¬ A ) ∧ (¬ B)] |
|---|---|---|---|---|
| True | True | False | False | True |
| True | False | False | False | True |
| False | True | False | False | True |
| False | False | True | True | True |
As $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ is a tautology, the statements are equivalent.
Inverse, Converse, and Contra-positive
Implication / if-then $(\rightarrow)$ is also called a conditional statement. It has two parts −
- Hypothesis, p
- Conclusion, q
As mentioned earlier, it is denoted as $p \rightarrow q$.
Example of Conditional Statement − If you do your homework, you will not be punished. Here, "you do your homework" is the hypothesis, p, and "you will not be punished" is the conclusion, q.
Inverse − An inverse of the conditional statement is the negation of both the hypothesis and the conclusion. If the statement is If p, then q, the inverse will be If not p, then not q. Thus the inverse of $p \rightarrow q$ is $ \lnot p \rightarrow \lnot q$.
Example − The inverse of If you do your homework, you will not be punished is If you do not do your homework, you will be punished.
Converse − The converse of the conditional statement is computed by interchanging the hypothesis and the conclusion. If the statement is If p, then q, the converse will be If q, then p. The converse of $p \rightarrow q$ is $q \rightarrow p$.
Example − The converse of "If you do your homework, you will not be punished" is "If you will not be punished, you do your homework.
Contra-positive − The contra-positive of the conditional is computed by interchanging the hypothesis and the conclusion of the inverse statement. If the statement is If p, then q, the contra-positive will be If not q, then not p. The contra-positive of $p \rightarrow q$ is $\lnot q \rightarrow \lnot p$.
Example − The Contra-positive of " If you do your homework, you will not be punished is "If you are punished, you did not do your homework.
Duality Principle
Duality principle states that for any true statement, the dual statement obtained by interchanging unions into intersections (and vice versa) and interchanging Universal set into Null set (and vice versa) is also true. If dual of any statement is the statement itself, it is said self-dual statement.
Example − The dual of $(A \cap B ) \cup C$ is $(A \cup B) \cap C$
Normal Forms
We can convert any proposition in two normal forms −
- Conjunctive normal form
- Disjunctive normal form
Conjunctive Normal Form
A compound statement is in conjunctive normal form if it is obtained by operating AND among variables (negation of variables included) connected with ORs. In terms of set operations, it is a compound statement obtained by Intersection among variables connected with Unions.
Examples
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
Disjunctive Normal Form
A compound statement is in disjunctive normal form if it is obtained by operating OR among variables (negation of variables included) connected with ANDs. In terms of set operations, it is a compound statement obtained by Union among variables connected with Intersections.
Examples
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
Discrete Mathematics - Predicate Logic
Predicate Logic deals with predicates, which are propositions containing variables.
Predicate Logic Definition
A predicate is an expression of one or more variables defined on some specific domain. A predicate with variables can be made a proposition by either assigning a value to the variable or by quantifying the variable.
The following are some examples of predicates −
- Let E(x, y) denote "x = y"
- Let X(a, b, c) denote "a + b + c = 0"
- Let M(x, y) denote "x is married to y"
Well Formed Formula
Well Formed Formula (wff) is a predicate holding any of the following −
All propositional constants and propositional variables are wffs
If x is a variable and Y is a wff, $\forall x Y$ and $\exists x Y$ are also wff
Truth value and false values are wffs
Each atomic formula is a wff
All connectives connecting wffs are wffs
Quantifiers
The variable of predicates is quantified by quantifiers. There are two types of quantifier in predicate logic − Universal Quantifier and Existential Quantifier.
Universal Quantifier
Universal quantifier states that the statements within its scope are true for every value of the specific variable. It is denoted by the symbol $\forall$.
$\forall x P(x)$ is read as for every value of x, P(x) is true.
Example − "Man is mortal" can be transformed into the propositional form $\forall x P(x)$ where P(x) is the predicate which denotes x is mortal and the universe of discourse is all men.
Existential Quantifier
Existential quantifier states that the statements within its scope are true for some values of the specific variable. It is denoted by the symbol $\exists $.
$\exists x P(x)$ is read as for some values of x, P(x) is true.
Example − "Some people are dishonest" can be transformed into the propositional form $\exists x P(x)$ where P(x) is the predicate which denotes x is dishonest and the universe of discourse is some people.
Nested Quantifiers
If we use a quantifier that appears within the scope of another quantifier, it is called nested quantifier.
Example
$\forall\ a\: \exists b\: P (x, y)$ where $P (a, b)$ denotes $a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ where $P (a, b)$ denotes $a + (b + c) = (a + b) + c$
Note − $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
Discrete Mathematics - Rules of Inference
To deduce new statements from the statements whose truth that we already know, Rules of Inference are used.
What are Rules of Inference for?
Mathematical logic is often used for logical proofs. Proofs are valid arguments that determine the truth values of mathematical statements.
An argument is a sequence of statements. The last statement is the conclusion and all its preceding statements are called premises (or hypothesis). The symbol $\therefore$, (read therefore) is placed before the conclusion. A valid argument is one where the conclusion follows from the truth values of the premises.
Rules of Inference provide the templates or guidelines for constructing valid arguments from the statements that we already have.
Table of Rules of Inference
| Rule of Inference | Name | Rule of Inference | Name |
|---|---|---|---|
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ |
Addition |
$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$ |
Disjunctive Syllogism |
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ |
Conjunction |
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$ |
Hypothetical Syllogism |
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$ |
Simplification |
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$ |
Constructive Dilemma |
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$ |
Modus Ponens |
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$ |
Destructive Dilemma |
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$ |
Modus Tollens |
Addition
If P is a premise, we can use Addition rule to derive $ P \lor Q $.
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$
Example
Let P be the proposition, He studies very hard is true
Therefore − "Either he studies very hard Or he is a very bad student." Here Q is the proposition he is a very bad student.
Conjunction
If P and Q are two premises, we can use Conjunction rule to derive $ P \land Q $.
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$
Example
Let P − He studies very hard
Let Q − He is the best boy in the class
Therefore − "He studies very hard and he is the best boy in the class"
Simplification
If $P \land Q$ is a premise, we can use Simplification rule to derive P.
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$
Example
"He studies very hard and he is the best boy in the class", $P \land Q$
Therefore − "He studies very hard"
Modus Ponens
If P and $P \rightarrow Q$ are two premises, we can use Modus Ponens to derive Q.
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$
Example
"If you have a password, then you can log on to facebook", $P \rightarrow Q$
"You have a password", P
Therefore − "You can log on to facebook"
Modus Tollens
If $P \rightarrow Q$ and $\lnot Q$ are two premises, we can use Modus Tollens to derive $\lnot P$.
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$
Example
"If you have a password, then you can log on to facebook", $P \rightarrow Q$
"You cannot log on to facebook", $\lnot Q$
Therefore − "You do not have a password "
Disjunctive Syllogism
If $\lnot P$ and $P \lor Q$ are two premises, we can use Disjunctive Syllogism to derive Q.
$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$
Example
"The ice cream is not vanilla flavored", $\lnot P$
"The ice cream is either vanilla flavored or chocolate flavored", $P \lor Q$
Therefore − "The ice cream is chocolate flavored
Hypothetical Syllogism
If $P \rightarrow Q$ and $Q \rightarrow R$ are two premises, we can use Hypothetical Syllogism to derive $P \rightarrow R$
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$
Example
"If it rains, I shall not go to school, $P \rightarrow Q$
"If I don't go to school, I won't need to do homework", $Q \rightarrow R$
Therefore − "If it rains, I won't need to do homework"
Constructive Dilemma
If $( P \rightarrow Q ) \land (R \rightarrow S)$ and $P \lor R$ are two premises, we can use constructive dilemma to derive $Q \lor S$.
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$
Example
If it rains, I will take a leave, $( P \rightarrow Q )$
If it is hot outside, I will go for a shower, $(R \rightarrow S)$
Either it will rain or it is hot outside, $P \lor R$
Therefore − "I will take a leave or I will go for a shower"
Destructive Dilemma
If $(P \rightarrow Q) \land (R \rightarrow S)$ and $ \lnot Q \lor \lnot S $ are two premises, we can use destructive dilemma to derive $\lnot P \lor \lnot R$.
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$
Example
If it rains, I will take a leave, $(P \rightarrow Q )$
If it is hot outside, I will go for a shower, $(R \rightarrow S)$
Either I will not take a leave or I will not go for a shower, $\lnot Q \lor \lnot S$
Therefore − "Either it does not rain or it is not hot outside"
Operators & Postulates
Group Theory is a branch of mathematics and abstract algebra that defines an algebraic structure named as group. Generally, a group comprises of a set of elements and an operation over any two elements on that set to form a third element also in that set.
In 1854, Arthur Cayley, the British Mathematician, gave the modern definition of group for the first time −
A set of symbols all of them different, and such that the product of any two of them (no matter in what order), or the product of any one of them into itself, belongs to the set, is said to be a group. These symbols are not in general convertible [commutative], but are associative.
In this chapter, we will know about operators and postulates that form the basics of set theory, group theory and Boolean algebra.
Any set of elements in a mathematical system may be defined with a set of operators and a number of postulates.
A binary operator defined on a set of elements is a rule that assigns to each pair of elements a unique element from that set. For example, given the set $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, we can say $\otimes$ is a binary operator for the operation $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.
The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −
Closure
A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.
Example
Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.
The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.
Associative Laws
A binary operator $\otimes$ on a set A is associative when it holds the following property −
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace$
The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.
The operator minus $( - )$ is not associative since
$$( x - y ) - z \ne x - ( y - z )$$
Commutative Laws
A binary operator $\otimes$ on a set A is commutative when it holds the following property −
$x \otimes y = y \otimes x$, where $x, y \in A$
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace$
The operator plus $( + )$ is commutative because for any two elements, $x,y \in A$, the property $x + y = y + x$ holds.
The operator minus $( - )$ is not associative since
$$x - y \ne y - x$$
Distributive Laws
Two binary operators $\otimes$ and $\circledast$ on a set A, are distributive over operator $\circledast$ when the following property holds −
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, where $x, y, z \in A $
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace$
The operators into $( * )$ and plus $( + )$ are distributive over operator + because for any three elements, $x,y,z \in A$, the property $x * ( y + z ) = ( x * y ) + ( x * z )$ holds.
However, these operators are not distributive over $*$ since
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
Identity Element
A set A has an identity element with respect to a binary operation $\otimes$ on A, if there exists an element $e \in A$, such that the following property holds −
$e \otimes x = x \otimes e$, where $x \in A$
Example
Let $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
The element 1 is an identity element with respect to operation $*$ since for any element $x \in Z$,
$$1 * x = x * 1$$
On the other hand, there is no identity element for the operation minus $( - )$
Inverse
If a set A has an identity element $e$ with respect to a binary operator $\otimes $, it is said to have an inverse whenever for every element $x \in A$, there exists another element $y \in A$, such that the following property holds −
$$x \otimes y = e$$
Example
Let $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
Given the operation plus $( + )$ and $e = 0$, the inverse of any element x is $(-x)$ since $x + (x) = 0$
De Morgan's Law
De Morgans Laws gives a pair of transformations between union and intersection of two (or more) sets in terms of their complements. The laws are −
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$, and
Universal set $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
Thus, we see that $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
Thus, we see that $(A \cap B)' = A' \cup B'$
Discrete Mathematics - Group Theory
Semigroup
A finite or infinite set $S$ with a binary operation $\omicron$ (Composition) is called semigroup if it holds following two conditions simultaneously −
Closure − For every pair $(a, b) \in S, \:(a \omicron b)$ has to be present in the set $S$.
Associative − For every element $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ must hold.
Example
The set of positive integers (excluding zero) with addition operation is a semigroup. For example, $ S = \lbrace 1, 2, 3, \dots \rbrace $
Here closure property holds as for every pair $(a, b) \in S, (a + b)$ is present in the set S. For example, $1 + 2 = 3 \in S]$
Associative property also holds for every element $a, b, c \in S, (a + b) + c = a + (b + c)$. For example, $(1 + 2) + 3 = 1 + (2 + 3) = 5$
Monoid
A monoid is a semigroup with an identity element. The identity element (denoted by $e$ or E) of a set S is an element such that $(a \omicron e) = a$, for every element $a \in S$. An identity element is also called a unit element. So, a monoid holds three properties simultaneously − Closure, Associative, Identity element.
Example
The set of positive integers (excluding zero) with multiplication operation is a monoid. $S = \lbrace 1, 2, 3, \dots \rbrace $
Here closure property holds as for every pair $(a, b) \in S, (a \times b)$ is present in the set S. [For example, $1 \times 2 = 2 \in S$ and so on]
Associative property also holds for every element $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [For example, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ and so on]
Identity property also holds for every element $a \in S, (a \times e) = a$ [For example, $(2 \times 1) = 2, (3 \times 1) = 3$ and so on]. Here identity element is 1.
Group
A group is a monoid with an inverse element. The inverse element (denoted by I) of a set S is an element such that $(a \omicron I) = (I \omicron a) = a$, for each element $a \in S$. So, a group holds four properties simultaneously - i) Closure, ii) Associative, iii) Identity element, iv) Inverse element. The order of a group G is the number of elements in G and the order of an element in a group is the least positive integer n such that an is the identity element of that group G.
Examples
The set of $N \times N$ non-singular matrices form a group under matrix multiplication operation.
The product of two $N \times N$ non-singular matrices is also an $N \times N$ non-singular matrix which holds closure property.
Matrix multiplication itself is associative. Hence, associative property holds.
The set of $N \times N$ non-singular matrices contains the identity matrix holding the identity element property.
As all the matrices are non-singular they all have inverse elements which are also nonsingular matrices. Hence, inverse property also holds.
Abelian Group
An abelian group G is a group for which the element pair $(a,b) \in G$ always holds commutative law. So, a group holds five properties simultaneously - i) Closure, ii) Associative, iii) Identity element, iv) Inverse element, v) Commutative.
Example
The set of positive integers (including zero) with addition operation is an abelian group. $G = \lbrace 0, 1, 2, 3, \dots \rbrace$
Here closure property holds as for every pair $(a, b) \in S, (a + b)$ is present in the set S. [For example, $1 + 2 = 2 \in S$ and so on]
Associative property also holds for every element $a, b, c \in S, (a + b) + c = a + (b + c)$ [For example, $(1 +2) + 3 = 1 + (2 + 3) = 6$ and so on]
Identity property also holds for every element $a \in S, (a \times e) = a$ [For example, $(2 \times 1) = 2, (3 \times 1) = 3$ and so on]. Here, identity element is 1.
Commutative property also holds for every element $a \in S, (a \times b) = (b \times a)$ [For example, $(2 \times 3) = (3 \times 2) = 3$ and so on]
Cyclic Group and Subgroup
A cyclic group is a group that can be generated by a single element. Every element of a cyclic group is a power of some specific element which is called a generator. A cyclic group can be generated by a generator g, such that every other element of the group can be written as a power of the generator g.
Example
The set of complex numbers $\lbrace 1,-1, i, -i \rbrace$ under multiplication operation is a cyclic group.
There are two generators − $i$ and $i$ as $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ and also $(i)^1 = -i, (i)^2 = -1, (i)^3 = i, (i)^4 = 1$ which covers all the elements of the group. Hence, it is a cyclic group.
Note − A cyclic group is always an abelian group but not every abelian group is a cyclic group. The rational numbers under addition is not cyclic but is abelian.
A subgroup H is a subset of a group G (denoted by $H G$) if it satisfies the four properties simultaneously − Closure, Associative, Identity element, and Inverse.
A subgroup H of a group G that does not include the whole group G is called a proper subgroup (Denoted by $H < G$). A subgroup of a cyclic group is cyclic and a abelian subgroup is also abelian.
Example
Let a group $G = \lbrace 1, i, -1, -i \rbrace$
Then some subgroups are $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,
This is not a subgroup − $H_3 = \lbrace 1, i \rbrace$ because that $(i)^{-1} = -i$ is not in $H_3$
Partially Ordered Set (POSET)
A partially ordered set consists of a set with a binary relation which is reflexive, antisymmetric and transitive. "Partially ordered set" is abbreviated as POSET.
Examples
-
The set of real numbers under binary operation less than or equal to $(\le)$ is a poset.
Let the set $S = \lbrace 1, 2, 3 \rbrace$ and the operation is $\le$
The relations will be $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
This relation R is reflexive as $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$
This relation R is anti-symmetric, as
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$
This relation R is also transitive as $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$.
Hence, it is a poset.
The vertex set of a directed acyclic graph under the operation reachability is a poset.
Hasse Diagram
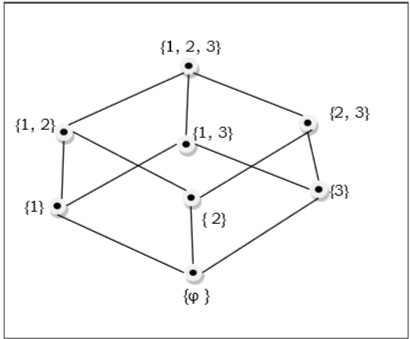
The Hasse diagram of a poset is the directed graph whose vertices are the element of that poset and the arcs covers the pairs (x, y) in the poset. If in the poset $x < y$, then the point x appears lower than the point y in the Hasse diagram. If $x<y<z$ in the poset, then the arrow is not shown between x and z as it is implicit.
Example
The poset of subsets of $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ is shown by the following Hasse diagram −
Linearly Ordered Set
A Linearly ordered set or Total ordered set is a partial order set in which every pair of element is comparable. The elements $a, b \in S$ are said to be comparable if either $a \le b$ or $b \le a$ holds. Trichotomy law defines this total ordered set. A totally ordered set can be defined as a distributive lattice having the property $\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ for all values of a and b in set S.
Example
The powerset of $\lbrace a, b \rbrace$ ordered by \subseteq is a totally ordered set as all the elements of the power set $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ are comparable.
Example of non-total order set
A set $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ under operation x divides y is not a total ordered set.
Here, for all $(x, y) \in S, x | y$ have to hold but it is not true that 2 | 3, as 2 does not divide 3 or 3 does not divide 2. Hence, it is not a total ordered set.
Lattice
A lattice is a poset $(L, \le)$ for which every pair $\lbrace a, b \rbrace \in L$ has a least upper bound (denoted by $a \lor b$) and a greatest lower bound (denoted by $a \land b$). LUB $(\lbrace a,b \rbrace)$ is called the join of a and b. GLB $(\lbrace a,b \rbrace )$ is called the meet of a and b.
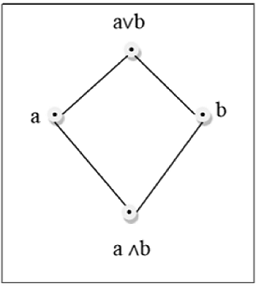
Example
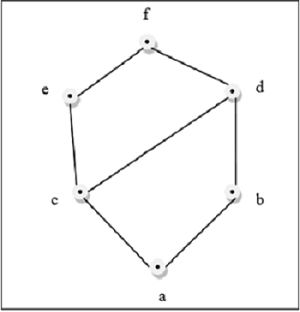
This above figure is a lattice because for every pair $\lbrace a, b \rbrace \in L$, a GLB and a LUB exists.
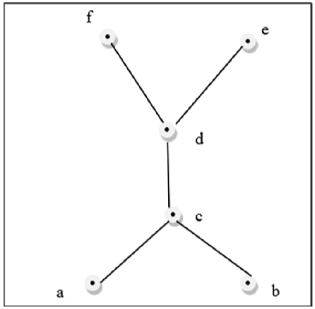
This above figure is a not a lattice because $GLB (a, b)$ and $LUB (e, f)$ does not exist.
Some other lattices are discussed below −
Bounded Lattice
A lattice L becomes a bounded lattice if it has a greatest element 1 and a least element 0.
Complemented Lattice
A lattice L becomes a complemented lattice if it is a bounded lattice and if every element in the lattice has a complement. An element x has a complement x if $\exists x(x \land x=0 and x \lor x = 1)$
Distributive Lattice
If a lattice satisfies the following two distribute properties, it is called a distributive lattice.
$a \lor (b \land c) = (a \lor b) \land (a \lor c)$
$a \land (b \lor c) = (a \land b) \lor (a \land c)$
Modular Lattice
If a lattice satisfies the following property, it is called modular lattice.
$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$
Properties of Lattices
Idempotent Properties
$a \lor a = a$
$a \land a = a$
Absorption Properties
$a \lor (a \land b) = a$
$a \land (a \lor b) = a$
Commutative Properties
$a \lor b = b \lor a$
$a \land b = b \land a$
Associative Properties
$a \lor (b \lor c) = (a \lor b) \lor c$
$a \land (b \land c) = (a \land b) \land c$
Dual of a Lattice
The dual of a lattice is obtained by interchanging the '$\lor$' and '$\land$' operations.
Example
The dual of $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$
Discrete Mathematics - Counting Theory
In daily lives, many a times one needs to find out the number of all possible outcomes for a series of events. For instance, in how many ways can a panel of judges comprising of 6 men and 4 women be chosen from among 50 men and 38 women? How many different 10 lettered PAN numbers can be generated such that the first five letters are capital alphabets, the next four are digits and the last is again a capital letter. For solving these problems, mathematical theory of counting are used. Counting mainly encompasses fundamental counting rule, the permutation rule, and the combination rule.
The Rules of Sum and Product
The Rule of Sum and Rule of Product are used to decompose difficult counting problems into simple problems.
The Rule of Sum − If a sequence of tasks $T_1, T_2, \dots, T_m$ can be done in $w_1, w_2, \dots w_m$ ways respectively (the condition is that no tasks can be performed simultaneously), then the number of ways to do one of these tasks is $w_1 + w_2 + \dots +w_m$. If we consider two tasks A and B which are disjoint (i.e. $A \cap B = \emptyset$), then mathematically $|A \cup B| = |A| + |B|$
The Rule of Product − If a sequence of tasks $T_1, T_2, \dots, T_m$ can be done in $w_1, w_2, \dots w_m$ ways respectively and every task arrives after the occurrence of the previous task, then there are $w_1 \times w_2 \times \dots \times w_m$ ways to perform the tasks. Mathematically, if a task B arrives after a task A, then $|A \times B| = |A|\times|B|$
Example
Question − A boy lives at X and wants to go to School at Z. From his home X he has to first reach Y and then Y to Z. He may go X to Y by either 3 bus routes or 2 train routes. From there, he can either choose 4 bus routes or 5 train routes to reach Z. How many ways are there to go from X to Z?
Solution − From X to Y, he can go in $3 + 2 = 5$ ways (Rule of Sum). Thereafter, he can go Y to Z in $4 + 5 = 9$ ways (Rule of Sum). Hence from X to Z he can go in $5 \times 9 = 45$ ways (Rule of Product).
Permutations
A permutation is an arrangement of some elements in which order matters. In other words a Permutation is an ordered Combination of elements.
Examples
-
From a set S ={x, y, z} by taking two at a time, all permutations are −
$ xy, yx, xz, zx, yz, zy $.
We have to form a permutation of three digit numbers from a set of numbers $S = \lbrace 1, 2, 3 \rbrace$. Different three digit numbers will be formed when we arrange the digits. The permutation will be = 123, 132, 213, 231, 312, 321
Number of Permutations
The number of permutations of n different things taken r at a time is denoted by $n_{P_{r}}$
$$n_{P_{r}} = \frac{n!}{(n - r)!}$$
where $n! = 1.2.3. \dots (n - 1).n$
Proof − Let there be n different elements.
There are n number of ways to fill up the first place. After filling the first place (n-1) number of elements is left. Hence, there are (n-1) ways to fill up the second place. After filling the first and second place, (n-2) number of elements is left. Hence, there are (n-2) ways to fill up the third place. We can now generalize the number of ways to fill up r-th place as [n (r1)] = nr+1
So, the total no. of ways to fill up from first place up to r-th-place −
$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$
$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$
Hence,
$n_{ P_{ r } } = n! / (n-r)!$
Some important formulas of permutation
-
If there are n elements of which $a_1$ are alike of some kind, $a_2$ are alike of another kind; $a_3$ are alike of third kind and so on and $a_r$ are of $r^{th}$ kind, where $(a_1 + a_2 + ... a_r) = n$.
Then, number of permutations of these n objects is = $n! / [(a_1!(a_2!) \dots (a_r!)]$.
Number of permutations of n distinct elements taking n elements at a time = $n_{P_n} = n!$
The number of permutations of n dissimilar elements taking r elements at a time, when x particular things always occupy definite places = $n-x_{p_{r-x}}$
The number of permutations of n dissimilar elements when r specified things always come together is − $r! (nr+1)!$
The number of permutations of n dissimilar elements when r specified things never come together is − $n![r! (nr+1)!]$
The number of circular permutations of n different elements taken x elements at time = $^np_{x}/x$
The number of circular permutations of n different things = $^np_{n}/n$
Some Problems
Problem 1 − From a bunch of 6 different cards, how many ways we can permute it?
Solution − As we are taking 6 cards at a time from a deck of 6 cards, the permutation will be $^6P_{6} = 6! = 720$
Problem 2 − In how many ways can the letters of the word 'READER' be arranged?
Solution − There are 6 letters word (2 E, 1 A, 1D and 2R.) in the word 'READER'.
The permutation will be $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$
Problem 3 − In how ways can the letters of the word 'ORANGE' be arranged so that the consonants occupy only the even positions?
Solution − There are 3 vowels and 3 consonants in the word 'ORANGE'. Number of ways of arranging the consonants among themselves $= ^3P_{3} = 3! = 6$. The remaining 3 vacant places will be filled up by 3 vowels in $^3P_{3} = 3! = 6$ ways. Hence, the total number of permutation is $6 \times 6 = 36$
Combinations
A combination is selection of some given elements in which order does not matter.
The number of all combinations of n things, taken r at a time is −
$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$
Problem 1
Find the number of subsets of the set $\lbrace1, 2, 3, 4, 5, 6\rbrace$ having 3 elements.
Solution
The cardinality of the set is 6 and we have to choose 3 elements from the set. Here, the ordering does not matter. Hence, the number of subsets will be $^6C_{3} = 20$.
Problem 2
There are 6 men and 5 women in a room. In how many ways we can choose 3 men and 2 women from the room?
Solution
The number of ways to choose 3 men from 6 men is $^6C_{3}$ and the number of ways to choose 2 women from 5 women is $^5C_{2}$
Hence, the total number of ways is − $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$
Problem 3
How many ways can you choose 3 distinct groups of 3 students from total 9 students?
Solution
Let us number the groups as 1, 2 and 3
For choosing 3 students for 1st group, the number of ways − $^9C_{3}$
The number of ways for choosing 3 students for 2nd group after choosing 1st group − $^6C_{3}$
The number of ways for choosing 3 students for 3rd group after choosing 1st and 2nd group − $^3C_{3}$
Hence, the total number of ways $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$
Pascal's Identity
Pascal's identity, first derived by Blaise Pascal in 17th century, states that the number of ways to choose k elements from n elements is equal to the summation of number of ways to choose (k-1) elements from (n-1) elements and the number of ways to choose elements from n-1 elements.
Mathematically, for any positive integers k and n: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$
Proof −
$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$
$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$
$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$
$= (n-1)! \frac{ n } { k!(n-k)! }$
$= \frac{ n! } { k!(n-k)! }$
$= n_{ C_{ k } }$
Pigeonhole Principle
In 1834, German mathematician, Peter Gustav Lejeune Dirichlet, stated a principle which he called the drawer principle. Now, it is known as the pigeonhole principle.
Pigeonhole Principle states that if there are fewer pigeon holes than total number of pigeons and each pigeon is put in a pigeon hole, then there must be at least one pigeon hole with more than one pigeon. If n pigeons are put into m pigeonholes where n > m, there's a hole with more than one pigeon.
Examples
Ten men are in a room and they are taking part in handshakes. If each person shakes hands at least once and no man shakes the same mans hand more than once then two men took part in the same number of handshakes.
There must be at least two people in a class of 30 whose names start with the same alphabet.
The Inclusion-Exclusion principle
The Inclusion-exclusion principle computes the cardinal number of the union of multiple non-disjoint sets. For two sets A and B, the principle states −
$|A \cup B| = |A| + |B| - |A \cap B|$
For three sets A, B and C, the principle states −
$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$
The generalized formula -
$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\n-1}|A_1 \cap \dots \cap A_2|$
Problem 1
How many integers from 1 to 50 are multiples of 2 or 3 but not both?
Solution
From 1 to 100, there are $50/2 = 25$ numbers which are multiples of 2.
There are $50/3 = 16$ numbers which are multiples of 3.
There are $50/6 = 8$ numbers which are multiples of both 2 and 3.
So, $|A|=25$, $|B|=16$ and $|A \cap B|= 8$.
$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$
Problem 2
In a group of 50 students 24 like cold drinks and 36 like hot drinks and each student likes at least one of the two drinks. How many like both coffee and tea?
Solution
Let X be the set of students who like cold drinks and Y be the set of people who like hot drinks.
So, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$
$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$
Hence, there are 10 students who like both tea and coffee.
Discrete Mathematics - Probability
Closely related to the concepts of counting is Probability. We often try to guess the results of games of chance, like card games, slot machines, and lotteries; i.e. we try to find the likelihood or probability that a particular result with be obtained.
Probability can be conceptualized as finding the chance of occurrence of an event. Mathematically, it is the study of random processes and their outcomes. The laws of probability have a wide applicability in a variety of fields like genetics, weather forecasting, opinion polls, stock markets etc.
Basic Concepts
Probability theory was invented in the 17th century by two French mathematicians, Blaise Pascal and Pierre de Fermat, who were dealing with mathematical problems regarding of chance.
Before proceeding to details of probability, let us get the concept of some definitions.
Random Experiment − An experiment in which all possible outcomes are known and the exact output cannot be predicted in advance is called a random experiment. Tossing a fair coin is an example of random experiment.
Sample Space − When we perform an experiment, then the set S of all possible outcomes is called the sample space. If we toss a coin, the sample space $S = \left \{ H, T \right \}$
Event − Any subset of a sample space is called an event. After tossing a coin, getting Head on the top is an event.
The word "probability" means the chance of occurrence of a particular event. The best we can say is how likely they are to happen, using the idea of probability.
$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$
As the occurrence of any event varies between 0% and 100%, the probability varies between 0 and 1.
Steps to find the probability
Step 1 − Calculate all possible outcomes of the experiment.
Step 2 − Calculate the number of favorable outcomes of the experiment.
Step 3 − Apply the corresponding probability formula.
Tossing a Coin
If a coin is tossed, there are two possible outcomes − Heads $(H)$ or Tails $(T)$
So, Total number of outcomes = 2
Hence, the probability of getting a Head $(H)$ on top is 1/2 and the probability of getting a Tails $(T)$ on top is 1/2
Throwing a Dice
When a dice is thrown, six possible outcomes can be on the top − $1, 2, 3, 4, 5, 6$.
The probability of any one of the numbers is 1/6
The probability of getting even numbers is 3/6 = 1/2
The probability of getting odd numbers is 3/6 = 1/2
Taking Cards From a Deck
From a deck of 52 cards, if one card is picked find the probability of an ace being drawn and also find the probability of a diamond being drawn.
Total number of possible outcomes − 52
Outcomes of being an ace − 4
Probability of being an ace = 4/52 = 1/13
Probability of being a diamond = 13/52 = 1/4
Probability Axioms
The probability of an event always varies from 0 to 1. $[0 \leq P(x) \leq 1]$
For an impossible event the probability is 0 and for a certain event the probability is 1.
-
If the occurrence of one event is not influenced by another event, they are called mutually exclusive or disjoint.
If $A_1, A_2....A_n$ are mutually exclusive/disjoint events, then $P(A_i \cap A_j) = \emptyset $ for $i \ne j$ and $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$
Properties of Probability
-
If there are two events $x$ and $\overline{x}$which are complementary, then the probability of the complementary event is −
$$p(\overline{x}) = 1-p(x)$$
-
For two non-disjoint events A and B, the probability of the union of two events −
$P(A \cup B) = P(A) + P(B)$
If an event A is a subset of another event B (i.e. $A \subset B$), then the probability of A is less than or equal to the probability of B. Hence, $A \subset B$ implies $P(A) \leq p(B)$
Conditional Probability
The conditional probability of an event B is the probability that the event will occur given an event A has already occurred. This is written as $P(B|A)$.
Mathematically − $ P(B|A) = P(A \cap B)/ P(A)$
If event A and B are mutually exclusive, then the conditional probability of event B after the event A will be the probability of event B that is $P(B)$.
Problem 1
In a country 50% of all teenagers own a cycle and 30% of all teenagers own a bike and cycle. What is the probability that a teenager owns bike given that the teenager owns a cycle?
Solution
Let us assume A is the event of teenagers owning only a cycle and B is the event of teenagers owning only a bike.
So, $P(A) = 50/100 = 0.5$ and $P(A \cap B) = 30/100 = 0.3$ from the given problem.
$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$
Hence, the probability that a teenager owns bike given that the teenager owns a cycle is 60%.
Problem 2
In a class, 50% of all students play cricket and 25% of all students play cricket and volleyball. What is the probability that a student plays volleyball given that the student plays cricket?
Solution
Let us assume A is the event of students playing only cricket and B is the event of students playing only volleyball.
So, $P(A) = 50/100 =0.5$ and $P(A \cap B) = 25/ 100 =0.25$ from the given problem.
$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$
Hence, the probability that a student plays volleyball given that the student plays cricket is 50%.
Problem 3
Six good laptops and three defective laptops are mixed up. To find the defective laptops all of them are tested one-by-one at random. What is the probability to find both of the defective laptops in the first two pick?
Solution
Let A be the event that we find a defective laptop in the first test and B be the event that we find a defective laptop in the second test.
Hence, $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$
Bayes' Theorem
Theorem − If A and B are two mutually exclusive events, where $P(A)$ is the probability of A and $P(B)$ is the probability of B, $P(A | B)$ is the probability of A given that B is true. $P(B | A)$ is the probability of B given that A is true, then Bayes Theorem states −
$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$
Application of Bayes' Theorem
In situations where all the events of sample space are mutually exclusive events.
In situations where either $P( A_i \cap B )$ for each $A_i$ or $P( A_i )$ and $P(B|A_i)$ for each $A_i$ is known.
Problem
Consider three pen-stands. The first pen-stand contains 2 red pens and 3 blue pens; the second one has 3 red pens and 2 blue pens; and the third one has 4 red pens and 1 blue pen. There is equal probability of each pen-stand to be selected. If one pen is drawn at random, what is the probability that it is a red pen?
Solution
Let $A_i$ be the event that ith pen-stand is selected.
Here, i = 1,2,3.
Since probability for choosing a pen-stand is equal, $P(A_i) = 1/3$
Let B be the event that a red pen is drawn.
The probability that a red pen is chosen among the five pens of the first pen-stand,
$P(B|A_1) = 2/5$
The probability that a red pen is chosen among the five pens of the second pen-stand,
$P(B|A_2) = 3/5$
The probability that a red pen is chosen among the five pens of the third pen-stand,
$P(B|A_3) = 4/5$
According to Bayes' Theorem,
$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$
$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$
$= 3/5$
Mathematical Induction
Mathematical induction, is a technique for proving results or establishing statements for natural numbers. This part illustrates the method through a variety of examples.
Definition
Mathematical Induction is a mathematical technique which is used to prove a statement, a formula or a theorem is true for every natural number.
The technique involves two steps to prove a statement, as stated below −
Step 1(Base step) − It proves that a statement is true for the initial value.
Step 2(Inductive step) − It proves that if the statement is true for the nth iteration (or number n), then it is also true for (n+1)th iteration ( or number n+1).
How to Do It
Step 1 − Consider an initial value for which the statement is true. It is to be shown that the statement is true for n = initial value.
Step 2 − Assume the statement is true for any value of n = k. Then prove the statement is true for n = k+1. We actually break n = k+1 into two parts, one part is n = k (which is already proved) and try to prove the other part.
Problem 1
$3^n-1$ is a multiple of 2 for n = 1, 2, ...
Solution
Step 1 − For $n = 1, 3^1-1 = 3-1 = 2$ which is a multiple of 2
Step 2 − Let us assume $3^n-1$ is true for $n=k$, Hence, $3^k -1$ is true (It is an assumption)
We have to prove that $3^{k+1}-1$ is also a multiple of 2
$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$
The first part $(2 \times 3k)$ is certain to be a multiple of 2 and the second part $(3k -1)$ is also true as our previous assumption.
Hence, $3^{k+1} 1$ is a multiple of 2.
So, it is proved that $3^n 1$ is a multiple of 2.
Problem 2
$1 + 3 + 5 + ... + (2n-1) = n^2$ for $n = 1, 2, \dots $
Solution
Step 1 − For $n=1, 1 = 1^2$, Hence, step 1 is satisfied.
Step 2 − Let us assume the statement is true for $n=k$.
Hence, $1 + 3 + 5 + \dots + (2k-1) = k^2$ is true (It is an assumption)
We have to prove that $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ also holds
$1 + 3 + 5 + \dots + (2(k+1) - 1)$
$= 1 + 3 + 5 + \dots + (2k+2 - 1)$
$= 1 + 3 + 5 + \dots + (2k + 1)$
$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$
$= k^2 + (2k + 1)$
$= (k + 1)^2$
So, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ hold which satisfies the step 2.
Hence, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ is proved.
Problem 3
Prove that $(ab)^n = a^nb^n$ is true for every natural number $n$
Solution
Step 1 − For $n=1, (ab)^1 = a^1b^1 = ab$, Hence, step 1 is satisfied.
Step 2 − Let us assume the statement is true for $n=k$, Hence, $(ab)^k = a^kb^k$ is true (It is an assumption).
We have to prove that $(ab)^{k+1} = a^{k+1}b^{k+1}$ also hold
Given, $(ab)^k = a^k b^k$
Or, $(ab)^k (ab) = (a^k b^k ) (ab)$ [Multiplying both side by 'ab']
Or, $(ab)^{k+1} = (aa^k) ( bb^k)$
Or, $(ab)^{k+1} = (a^{k+1}b^{k+1})$
Hence, step 2 is proved.
So, $(ab)^n = a^nb^n$ is true for every natural number n.
Strong Induction
Strong Induction is another form of mathematical induction. Through this induction technique, we can prove that a propositional function, $P(n)$ is true for all positive integers, $n$, using the following steps −
Step 1(Base step) − It proves that the initial proposition $P(1)$ true.
Step 2(Inductive step) − It proves that the conditional statement $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ is true for positive integers $k$.
Discrete Mathematics - Recurrence Relation
In this chapter, we will discuss how recursive techniques can derive sequences and be used for solving counting problems. The procedure for finding the terms of a sequence in a recursive manner is called recurrence relation. We study the theory of linear recurrence relations and their solutions. Finally, we introduce generating functions for solving recurrence relations.
Definition
A recurrence relation is an equation that recursively defines a sequence where the next term is a function of the previous terms (Expressing $F_n$ as some combination of $F_i$ with $i < n$).
Example − Fibonacci series − $F_n = F_{n-1} + F_{n-2}$, Tower of Hanoi − $F_n = 2F_{n-1} + 1$
Linear Recurrence Relations
A linear recurrence equation of degree k or order k is a recurrence equation which is in the format $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ is a constant and $A_k \neq 0$) on a sequence of numbers as a first-degree polynomial.
These are some examples of linear recurrence equations −
| Recurrence relations | Initial values | Solutions |
|---|---|---|
| Fn = Fn-1 + Fn-2 | a1 = a2 = 1 | Fibonacci number |
| Fn = Fn-1 + Fn-2 | a1 = 1, a2 = 3 | Lucas Number |
| Fn = Fn-2 + Fn-3 | a1 = a2 = a3 = 1 | Padovan sequence |
| Fn = 2Fn-1 + Fn-2 | a1 = 0, a2 = 1 | Pell number |
How to solve linear recurrence relation
Suppose, a two ordered linear recurrence relation is − $F_n = AF_{n-1} +BF_{n-2}$ where A and B are real numbers.
The characteristic equation for the above recurrence relation is −
$$x^2 - Ax - B = 0$$
Three cases may occur while finding the roots −
Case 1 − If this equation factors as $(x- x_1)(x- x_1) = 0$ and it produces two distinct real roots $x_1$ and $x_2$, then $F_n = ax_1^n+ bx_2^n$ is the solution. [Here, a and b are constants]
Case 2 − If this equation factors as $(x- x_1)^2 = 0$ and it produces single real root $x_1$, then $F_n = a x_1^n+ bn x_1^n$ is the solution.
Case 3 − If the equation produces two distinct complex roots, $x_1$ and $x_2$ in polar form $x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta)$, then $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ is the solution.
Problem 1
Solve the recurrence relation $F_n = 5F_{n-1} - 6F_{n-2}$ where $F_0 = 1$ and $F_1 = 4$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 - 5x + 6 = 0,$$
So, $(x - 3) (x - 2) = 0$
Hence, the roots are −
$x_1 = 3$ and $x_2 = 2$
The roots are real and distinct. So, this is in the form of case 1
Hence, the solution is −
$$F_n = ax_1^n + bx_2^n$$
Here, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$
Therefore,
$1 = F_0 = a3^0 + b2^0 = a+b$
$4 = F_1 = a3^1 + b2^1 = 3a+2b$
Solving these two equations, we get $ a = 2$ and $b = -1$
Hence, the final solution is −
$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$
Problem 2
Solve the recurrence relation − $F_n = 10F_{n-1} - 25F_{n-2}$ where $F_0 = 3$ and $F_1 = 17$
Solution
The characteristic equation of the recurrence relation is −
$$ x^2 - 10x -25 = 0$$
So $(x - 5)^2 = 0$
Hence, there is single real root $x_1 = 5$
As there is single real valued root, this is in the form of case 2
Hence, the solution is −
$F_n = ax_1^n + bnx_1^n$
$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$
$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$
Solving these two equations, we get $a = 3$ and $b = 2/5$
Hence, the final solution is − $F_n = 3.5^n +( 2/5) .n.2^n $
Problem 3
Solve the recurrence relation $F_n = 2F_{n-1} - 2F_{n-2}$ where $F_0 = 1$ and $F_1 = 3$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 -2x -2 = 0$$
Hence, the roots are −
$x_1 = 1 + i$ and $x_2 = 1 - i$
In polar form,
$x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta),$ where $r = \sqrt 2$ and $\theta = \frac{\pi}{4}$
The roots are imaginary. So, this is in the form of case 3.
Hence, the solution is −
$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$
$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$
$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$
Solving these two equations we get $a = 1$ and $b = 2$
Hence, the final solution is −
$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$
Non-Homogeneous Recurrence Relation and Particular Solutions
A recurrence relation is called non-homogeneous if it is in the form
$F_n = AF_{n-1} + BF_{n-2} + f(n)$ where $f(n) \ne 0$
Its associated homogeneous recurrence relation is $F_n = AF_{n1} + BF_{n-2}$
The solution $(a_n)$ of a non-homogeneous recurrence relation has two parts.
First part is the solution $(a_h)$ of the associated homogeneous recurrence relation and the second part is the particular solution $(a_t)$.
$$a_n=a_h+a_t$$
Solution to the first part is done using the procedures discussed in the previous section.
To find the particular solution, we find an appropriate trial solution.
Let $f(n) = cx^n$ ; let $x^2 = Ax + B$ be the characteristic equation of the associated homogeneous recurrence relation and let $x_1$ and $x_2$ be its roots.
If $x \ne x_1$ and $x \ne x_2$, then $a_t = Ax^n$
If $x = x_1$, $x \ne x_2$, then $a_t = Anx^n$
If $x = x_1 = x_2$, then $a_t = An^2x^n$
Example
Let a non-homogeneous recurrence relation be $F_n = AF_{n1} + BF_{n-2} + f(n)$ with characteristic roots $x_1 = 2$ and $x_2 = 5$. Trial solutions for different possible values of $f(n)$ are as follows −