- Discrete Mathematics - Home
- Discrete Mathematics Introduction
- Mathematical Statements and Operations
- Atomic and Molecular Statements
- Implications
- Predicates and Quantifiers
- Sets
- Sets and Notations
- Relations
- Operations on Sets
- Venn Diagrams on Sets
- Functions
- Surjection and Bijection Functions
- Image and Inverse-Image
- Mathematical Logic
- Propositional Logic
- Logical Equivalence
- Deductions
- Predicate Logic
- Proof by Contrapositive
- Proof by Contradiction
- Proof by Cases
- Rules of Inference
- Group Theory
- Operators & Postulates
- Group Theory
- Algebric Structure for Groups
- Abelian Group
- Semi Group
- Monoid
- Rings and Subring
- Properties of Rings
- Integral Domain
- Fields
- Counting & Probability
- Counting Theory
- Combinatorics
- Additive and Multiplicative Principles
- Counting with Sets
- Inclusion and Exclusion
- Bit Strings
- Lattice Path
- Binomial Coefficients
- Pascal's Triangle
- Permutations and Combinations
- Pigeonhole Principle
- Probability Theory
- Probability
- Sample Space, Outcomes, Events
- Conditional Probability and Independence
- Random Variables in Probability Theory
- Distribution Functions in Probability Theory
- Variance and Standard Deviation
- Mathematical & Recurrence
- Mathematical Induction
- Formalizing Proofs for Mathematical Induction
- Strong and Weak Induction
- Recurrence Relation
- Linear Recurrence Relations
- Non-Homogeneous Recurrence Relations
- Solving Recurrence Relations
- Master's Theorem
- Generating Functions
- Graph Theory
- Graph & Graph Models
- More on Graphs
- Planar Graphs
- Non-Planar Graphs
- Polyhedra
- Introduction to Trees
- Properties of Trees
- Rooted and Unrooted Trees
- Spanning Trees
- Graph Coloring
- Coloring Theory in General
- Coloring Edges
- Euler Paths and Circuits
- Hamiltonion Path
- Boolean Algebra
- Boolean Expressions & Functions
- Simplification of Boolean Functions
- Advanced Topics
- Number Theory
- Divisibility
- Remainder Classes
- Properties of Congruence
- Solving Linear Diophantine Equation
- Useful Resources
- Quick Guide
- Useful Resources
- Discussion
Graph & Graph Models
The previous part brought forth the different tools for reasoning, proofing and problem solving. In this part, we will study the discrete structures that form the basis of formulating many a real-life problem.
The two discrete structures that we will cover are graphs and trees. A graph is a set of points, called nodes or vertices, which are interconnected by a set of lines called edges. The study of graphs, or graph theory is an important part of a number of disciplines in the fields of mathematics, engineering and computer science.
What is a Graph?
Definition − A graph (denoted as $G = (V, E)$) consists of a non-empty set of vertices or nodes V and a set of edges E.
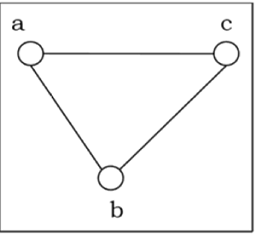
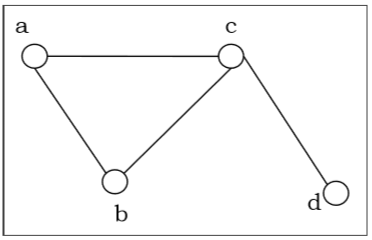
Example − Let us consider, a Graph is $G = (V, E)$ where $V = \lbrace a, b, c, d \rbrace $ and $E = \lbrace \lbrace a, b \rbrace, \lbrace a, c \rbrace, \lbrace b, c \rbrace, \lbrace c, d \rbrace \rbrace$
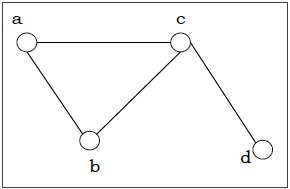
Degree of a Vertex − The degree of a vertex V of a graph G (denoted by deg (V)) is the number of edges incident with the vertex V.
| Vertex | Degree | Even / Odd |
|---|---|---|
| a | 2 | even |
| b | 2 | even |
| c | 3 | odd |
| d | 1 | odd |
Even and Odd Vertex − If the degree of a vertex is even, the vertex is called an even vertex and if the degree of a vertex is odd, the vertex is called an odd vertex.
Degree of a Graph − The degree of a graph is the largest vertex degree of that graph. For the above graph the degree of the graph is 3.
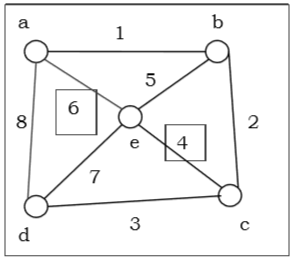
The Handshaking Lemma − In a graph, the sum of all the degrees of all the vertices is equal to twice the number of edges.
Types of Graphs
There are different types of graphs, which we will learn in the following section.
Null Graph
A null graph has no edges. The null graph of $n$ vertices is denoted by $N_n$
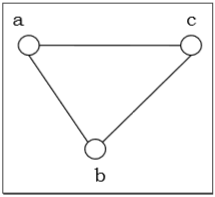
Simple Graph
A graph is called simple graph/strict graph if the graph is undirected and does not contain any loops or multiple edges.
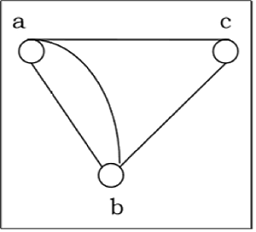
Multi-Graph
If in a graph multiple edges between the same set of vertices are allowed, it is called Multigraph. In other words, it is a graph having at least one loop or multiple edges.
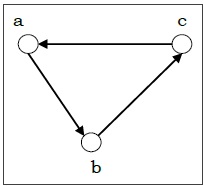
Directed and Undirected Graph
A graph $G = (V, E)$ is called a directed graph if the edge set is made of ordered vertex pair and a graph is called undirected if the edge set is made of unordered vertex pair.
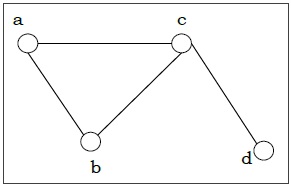
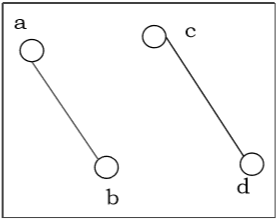
Connected and Disconnected Graph
A graph is connected if any two vertices of the graph are connected by a path; while a graph is disconnected if at least two vertices of the graph are not connected by a path. If a graph G is disconnected, then every maximal connected subgraph of $G$ is called a connected component of the graph $G$.
Regular Graph
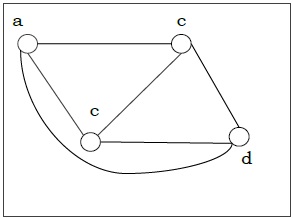
A graph is regular if all the vertices of the graph have the same degree. In a regular graph G of degree $r$, the degree of each vertex of $G$ is r.
Complete Graph
A graph is called complete graph if every two vertices pair are joined by exactly one edge. The complete graph with n vertices is denoted by $K_n$
Cycle Graph
If a graph consists of a single cycle, it is called cycle graph. The cycle graph with n vertices is denoted by $C_n$
Bipartite Graph
If the vertex-set of a graph G can be split into two disjoint sets, $V_1$ and $V_2$, in such a way that each edge in the graph joins a vertex in $V_1$ to a vertex in $V_2$, and there are no edges in G that connect two vertices in $V_1$ or two vertices in $V_2$, then the graph $G$ is called a bipartite graph.
Complete Bipartite Graph
A complete bipartite graph is a bipartite graph in which each vertex in the first set is joined to every single vertex in the second set. The complete bipartite graph is denoted by $K_{x,y}$ where the graph $G$ contains $x$ vertices in the first set and $y$ vertices in the second set.
Representation of Graphs
There are mainly two ways to represent a graph −
- Adjacency Matrix
- Adjacency List
Adjacency Matrix
An Adjacency Matrix $A[V][V]$ is a 2D array of size $V \times V$ where $V$ is the number of vertices in a undirected graph. If there is an edge between $V_x$ to $V_y$ then the value of $A[V_x][V_y]=1$ and $A[V_y][V_x]=1$, otherwise the value will be zero. And for a directed graph, if there is an edge between $V_x$ to $V_y$, then the value of $A[V_x][V_y]=1$, otherwise the value will be zero.
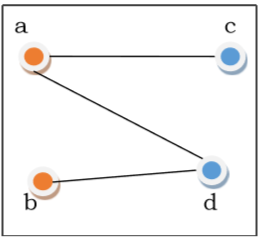
Adjacency Matrix of an Undirected Graph
Let us consider the following undirected graph and construct the adjacency matrix −
Adjacency matrix of the above undirected graph will be −
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
1 |
0 |
1 |
0 |
c |
1 |
1 |
0 |
1 |
d |
0 |
0 |
1 |
0 |
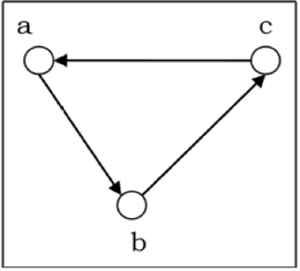
Adjacency Matrix of a Directed Graph
Let us consider the following directed graph and construct its adjacency matrix −
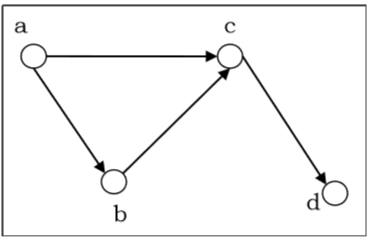
Adjacency matrix of the above directed graph will be −
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
0 |
0 |
1 |
0 |
c |
0 |
0 |
0 |
1 |
d |
0 |
0 |
0 |
0 |
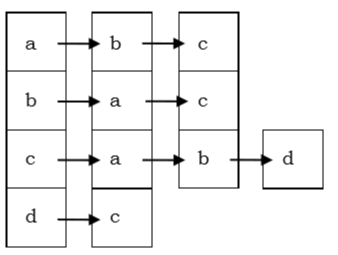
Adjacency List
In adjacency list, an array $(A[V])$ of linked lists is used to represent the graph G with $V$ number of vertices. An entry $A[V_x]$ represents the linked list of vertices adjacent to the $Vx-th$ vertex. The adjacency list of the undirected graph is as shown in the figure below −
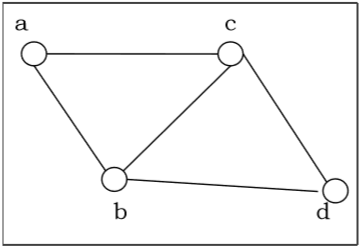
Planar vs. Non-planar graph
Planar graph − A graph $G$ is called a planar graph if it can be drawn in a plane without any edges crossed. If we draw graph in the plane without edge crossing, it is called embedding the graph in the plane.
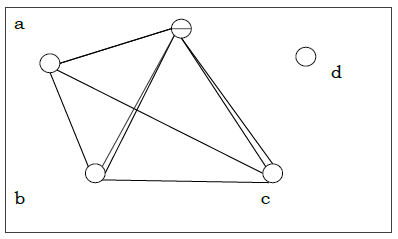
Non-planar graph − A graph is non-planar if it cannot be drawn in a plane without graph edges crossing.
Isomorphism
If two graphs G and H contain the same number of vertices connected in the same way, they are called isomorphic graphs (denoted by $G \cong H$).
It is easier to check non-isomorphism than isomorphism. If any of these following conditions occurs, then two graphs are non-isomorphic −
- The number of connected components are different
- Vertex-set cardinalities are different
- Edge-set cardinalities are different
- Degree sequences are different
Example
The following graphs are isomorphic −
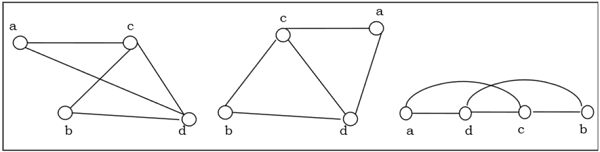
Homomorphism
A homomorphism from a graph $G$ to a graph $H$ is a mapping (May not be a bijective mapping)$ h: G \rightarrow H$ such that − $(x, y) \in E(G) \rightarrow (h(x), h(y)) \in E(H)$. It maps adjacent vertices of graph $G$ to the adjacent vertices of the graph $H$.
Properties of Homomorphisms
A homomorphism is an isomorphism if it is a bijective mapping.
Homomorphism always preserves edges and connectedness of a graph.
The compositions of homomorphisms are also homomorphisms.
To find out if there exists any homomorphic graph of another graph is a NPcomplete problem.
Euler Graphs
A connected graph $G$ is called an Euler graph, if there is a closed trail which includes every edge of the graph $G$. An Euler path is a path that uses every edge of a graph exactly once. An Euler path starts and ends at different vertices.
An Euler circuit is a circuit that uses every edge of a graph exactly once. An Euler circuit always starts and ends at the same vertex. A connected graph $G$ is an Euler graph if and only if all vertices of $G$ are of even degree, and a connected graph $G$ is Eulerian if and only if its edge set can be decomposed into cycles.
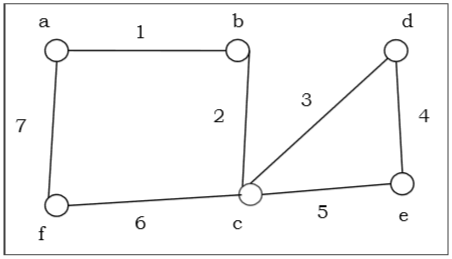
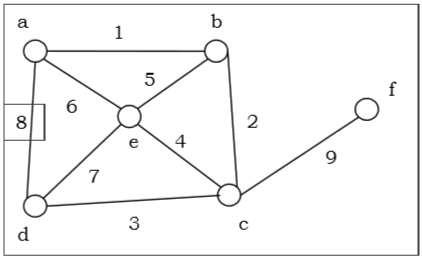
The above graph is an Euler graph as $a\: 1\: b\: 2\: c\: 3\: d\: 4\: e\: 5\: c\: 6\: f\: 7\: g$ covers all the edges of the graph.
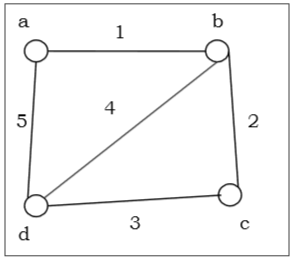
Hamiltonian Graphs
A connected graph $G$ is called Hamiltonian graph if there is a cycle which includes every vertex of $G$ and the cycle is called Hamiltonian cycle. Hamiltonian walk in graph $G$ is a walk that passes through each vertex exactly once.
If $G$ is a simple graph with n vertices, where $n \geq 3$ If $deg(v) \geq \frac{n}{2}$ for each vertex $v$, then the graph $G$ is Hamiltonian graph. This is called Dirac's Theorem.
If $G$ is a simple graph with $n$ vertices, where $n \geq 2$ if $deg(x) + deg(y) \geq n$ for each pair of non-adjacent vertices x and y, then the graph $G$ is Hamiltonian graph. This is called Ore's theorem.