
- Discrete Mathematics - Home
- Discrete Mathematics Introduction
- Mathematical Statements and Operations
- Atomic and Molecular Statements
- Implications
- Predicates and Quantifiers
- Sets
- Sets and Notations
- Relations
- Operations on Sets
- Venn Diagrams on Sets
- Functions
- Surjection and Bijection Functions
- Image and Inverse-Image
- Mathematical Logic
- Propositional Logic
- Logical Equivalence
- Deductions
- Predicate Logic
- Proof by Contrapositive
- Proof by Contradiction
- Proof by Cases
- Rules of Inference
- Group Theory
- Operators & Postulates
- Group Theory
- Algebric Structure for Groups
- Abelian Group
- Semi Group
- Monoid
- Rings and Subring
- Properties of Rings
- Integral Domain
- Fields
- Counting & Probability
- Counting Theory
- Combinatorics
- Additive and Multiplicative Principles
- Counting with Sets
- Inclusion and Exclusion
- Bit Strings
- Lattice Path
- Binomial Coefficients
- Pascal's Triangle
- Permutations and Combinations
- Pigeonhole Principle
- Probability Theory
- Probability
- Sample Space, Outcomes, Events
- Conditional Probability and Independence
- Random Variables in Probability Theory
- Distribution Functions in Probability Theory
- Variance and Standard Deviation
- Mathematical & Recurrence
- Mathematical Induction
- Formalizing Proofs for Mathematical Induction
- Strong and Weak Induction
- Recurrence Relation
- Linear Recurrence Relations
- Non-Homogeneous Recurrence Relations
- Solving Recurrence Relations
- Master's Theorem
- Generating Functions
- Graph Theory
- Graph & Graph Models
- More on Graphs
- Planar Graphs
- Non-Planar Graphs
- Polyhedra
- Introduction to Trees
- Properties of Trees
- Rooted and Unrooted Trees
- Spanning Trees
- Graph Coloring
- Coloring Theory in General
- Coloring Edges
- Euler Paths and Circuits
- Hamiltonion Path
- Boolean Algebra
- Boolean Expressions & Functions
- Simplification of Boolean Functions
- Advanced Topics
- Number Theory
- Divisibility
- Remainder Classes
- Properties of Congruence
- Solving Linear Diophantine Equation
- Useful Resources
- Quick Guide
- Useful Resources
- Discussion
Discrete Mathematics - Relations
Whenever sets are being discussed, the relationship between the elements of the sets is the next thing that comes up. Relations may exist between objects of the same set or between objects of two or more sets.
Definition and Properties
A binary relation R from set x to y (written as $xRy$ or $R(x,y)$) is a subset of the Cartesian product $x \times y$. If the ordered pair of G is reversed, the relation also changes.
Generally an n-ary relation R between sets $A_1, \dots ,\ and\ A_n$ is a subset of the n-ary product $A_1 \times \dots \times A_n$. The minimum cardinality of a relation R is Zero and maximum is $n^2$ in this case.
A binary relation R on a single set A is a subset of $A \times A$.
For two distinct sets, A and B, having cardinalities m and n respectively, the maximum cardinality of a relation R from A to B is mn.
Domain and Range
If there are two sets A and B, and relation R have order pair (x, y), then −
The domain of R, Dom(R), is the set $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$
The range of R, Ran(R), is the set $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$
Examples
Let, $A = \lbrace 1, 2, 9 \rbrace $ and $ B = \lbrace 1, 3, 7 \rbrace$
-
Case 1 − If relation R is 'equal to' then $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom(R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
-
Case 2 − If relation R is 'less than' then $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom(R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
-
Case 3 − If relation R is 'greater than' then $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom(R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
Representation of Relations using Graph
A relation can be represented using a directed graph.
The number of vertices in the graph is equal to the number of elements in the set from which the relation has been defined. For each ordered pair (x, y) in the relation R, there will be a directed edge from the vertex x to vertex y. If there is an ordered pair (x, x), there will be self- loop on vertex x.
Suppose, there is a relation $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ on set $S = \lbrace 1, 2, 3 \rbrace$, it can be represented by the following graph −
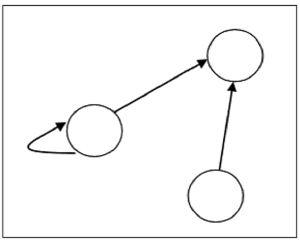
Types of Relations
The Empty Relation between sets X and Y, or on E, is the empty set $\emptyset$
The Full Relation between sets X and Y is the set $X \times Y$
The Identity Relation on set X is the set $\lbrace (x, x) | x \in X \rbrace$
-
The Inverse Relation R' of a relation R is defined as − $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
Example − If $R = \lbrace (1, 2), (2, 3) \rbrace$ then $R' $ will be $\lbrace (2, 1), (3, 2) \rbrace$
-
A relation R on set A is called Reflexive if $\forall a \in A$ is related to a (aRa holds)
Example − The relation $R = \lbrace (a, a), (b, b) \rbrace$ on set $X = \lbrace a, b \rbrace$ is reflexive.
-
A relation R on set A is called Irreflexive if no $a \in A$ is related to a (aRa does not hold).
Example − The relation $R = \lbrace (a, b), (b, a) \rbrace$ on set $X = \lbrace a, b \rbrace$ is irreflexive.
-
A relation R on set A is called Symmetric if $xRy$ implies $yRx$, $\forall x \in A$ and $\forall y \in A$.
Example − The relation $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ on set $A = \lbrace 1, 2, 3 \rbrace$ is symmetric.
-
A relation R on set A is called Anti-Symmetric if $xRy$ and $yRx$ implies $x = y \: \forall x \in A$ and $\forall y \in A$.
Example − The relation $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ is anti-symmetric since $x \leq y$ and $y \leq x$ implies $x = y$.
-
A relation R on set A is called Transitive if $xRy$ and $yRz$ implies $xRz, \forall x,y,z \in A$.
Example − The relation $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ on set $A = \lbrace 1, 2, 3 \rbrace$ is transitive.
-
A relation is an Equivalence Relation if it is reflexive, symmetric, and transitive.
Example − The relation $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ on set $A = \lbrace 1, 2, 3 \rbrace$ is an equivalence relation since it is reflexive, symmetric, and transitive.