Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Difference between Series Resonance and Parallel Resonance
In an AC electric circuit, when the capacitive reactance is balanced by the inductive reactance at some given frequency, then this condition in the circuit is referred as resonance. The frequency of the supply voltage at which resonance occurs in the circuit is called resonant frequency. At the resonance in the circuit, the reactance of the capacitor and inductor cancel each other. Also, at the condition of resonance, no reactive power is taken from the source.
Based on the arrangement of capacitor and inductor in the electric circuit, the resonance is divided in two types viz. −
- Series resonance
- Parallel resonance
In this article, we have described the differences between series resonance and parallel resonance. We also added a short description of series resonance and parallel resonance for your reference, which makes the understanding of differences easier.
What is Series Resonance?
When resistor (R), inductor (L) and capacitor (C) are connected in series, and at some frequency of supply voltage, the effect of inductor and capacitor cancel each other so that the circuit behaves like a pure resistive circuit, then this condition of the series circuit is known as series resonance.
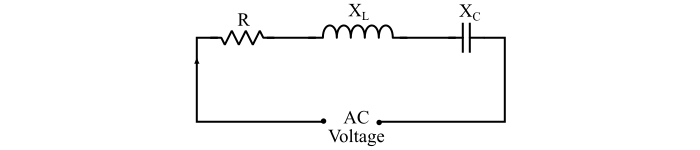
In series resonance, the inductive reactance (XL) and the capacitive reactance (XC) become equal, therefore, the total impedance of the series resonating circuit is equal the resistance of the circuit, i.e.
$$Z\:=\:R$$
Hence, at the series resonance condition, the circuit offers minimum impedance. Consequently, the value of electric current flowing through the circuit will be maximum. The series resonance results in the maximum admittance in the series RLC circuit.
Some common applications of series resonance are −
- Oscillator circuits
- Voltage amplifiers
- High frequency filters, etc.
What is Parallel Resonance?
When resistor (R), inductor (L) and capacitor (C) are connected in parallel and the effect of inductor cancels the effect of capacitor at a particular supply frequency, then this condition of the circuit is known as parallel resonance.
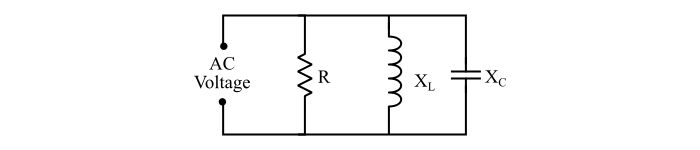
The parallel resonance causes maximum impedance in the circuit. As a result, the current flowing through the circuit at parallel resonance is minimum. As the parallel resonance eliminates the effect of capacitor and inductor from the circuit, thus the circuit behaves like a pure resistive circuit. The parallel resonance is also used in many applications such as:
- Current amplifiers
- Filter circuits
- Radio frequency amplifiers
- Induction heating systems, etc.
Difference between Series Resonance and Parallel Resonance
The key differences between series resonance and parallel resonance are given in the following table −
| Basis of Difference | Series Resonance | Parallel Resonance |
|---|---|---|
| Definition | When a resistor, inductor and capacitor are connected in series across an AC supply and the inductor and capacitor cancel the effect of each other at a particular frequency, then this condition of the series circuit is known as series resonance. | A combination of a resistor, inductor and a capacitor is connected across an AC source and the inductor and capacitor cancel the effect of each other at a specific supply frequency, then this condition of the parallel RLC circuit is known as parallel resonance. |
| Impedance | The impedance of a series RLC circuit becomes minimum at series resonance. | The impedance of a parallel RLC circuit becomes maximum at parallel resonance. |
| Admittance | The series RLC circuit offers maximum admittance at series resonance. | The admittance of the parallel RLC circuit at parallel resonance is minimum. |
| Current | The series resonance results in the maximum current through the circuit. | The current in circuit at parallel resonance is minimum. |
| Behave of the circuit | The series RLC circuit behaves as an accepter circuit at series resonance. | The parallel RLC circuit acts as a rejector circuit at parallel resonance |
| Magnify | The series resonance magnifies the voltage in the circuit. | The parallel resonance magnifies the current in the circuit. |
| Equation of effective impedance | The effective impedance of series RLC circuit at series resonance is given by, $$Z\:=\:R$$ | The effective impedance of parallel RLC circuit at parallel resonance is given by, $$Z\:=\:\frac{L}{CR}$$ |
| Quality factor (Q-factor) | For series resonance, the quality factor is given by, $$Q-\mathrm{factor}\:=\:\frac{\omega_{0}L}{R}\:=\:\frac{1}{\omega_{0}RC}$$ | For parallel resonance, the quality factor is given by, $$Q-\mathrm{factor}\:=\:\frac{R}{\omega_{0}L}\:=\omega_{0}RC$$ |
| Applications | The series resonance is widely used in tuning, oscillator circuits, voltage amplifiers, high frequency filters, etc. | The parallel resonance is used in current amplifiers, induction heating, filters, radio-frequency amplifiers, etc. |
Conclusion
In this article, we have highlighted several differences between series resonance and parallel resonance by considering various parameters such as basic definition, impedance, current, applications, etc. The major difference between series resonance and parallel resonance is that a series resonance results in the minimum impedance and maximum current flow in the circuit, while a parallel resonance results in maximum impedance and minimum current flow in the circuit.
31K+ Views
