
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Represent Graph Using Incidence Matrix
What is incidence matrix?
An incidence matrix is a mathematical representation of a graph that shows the relationship between vertices and edges. In other words, it is a matrix M of size v x e, where v = number of vertices and e = number of edges. For example, if the graph has an edge number n from vertex i to vertex j, then in the incidence matrix at ith row and nth column it will be 1.
Graph
The image below represent a simple undirected graph with 6 vertices and 8 edges.
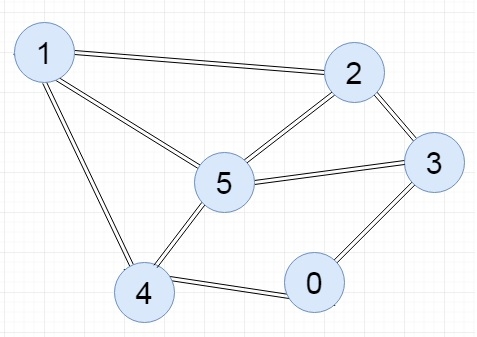
Incidence Matrix
The incidence matrix of the above graph is shown below.
| E0 |
E1 |
E2 |
E3 |
E4 |
E5 |
E6 |
E7 |
E8 |
|
|---|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
| 2 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
| 3 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
| 4 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
| 5 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
Algorithm
The following are the steps to represent a graph using an incidence matrix:
- Step 1: Start
- Step 2: Input the number of vertices V and number of edges E in the graph
- Step 3: Initialize a V x E matrix (incMatrix) and set all values to 0.
- Step 4: For each edge, repeat the steps 5,6 and 7.
- Step 5: Input the pair of vertices (u, v) that the edge connects
- Step 6: If the graph is undirected,set incMatrix[u][edge] = 1 and set incMatrix[v][edge] = 1
- Step 7: If the graph is directed,set incMatrix[u][edge] = -1 (edge leaves u) and set incMatrix[v][edge] = 1 (edge enters v)
- Step 8: Display the incidence matrix.
- Step 9: End
C++ Program for Incidence Matrix Representation of a Graph
In the code below we will be implementing the Incidence Matrix Representation of a Graph in C++:
#include <iostream>
using namespace std;
int main() {
int V, E;
bool isDirected;
// Step 1 & 2: Input vertices and edges
cout << "Enter number of vertices: ";
cin >> V;
cout << "Enter number of edges: ";
cin >> E;
cout << "Is the graph directed? (1 for Yes, 0 for No): ";
cin >> isDirected;
// Step 3: Initialize incidence matrix
int incMatrix[V][E];
for (int i = 0; i < V; i++)
for (int j = 0; j < E; j++)
incMatrix[i][j] = 0;
// Step 4: Input edges
for (int e = 0; e < E; e++) {
int u, v;
cout << "Enter edge " << e + 1 << " (format: u v): ";
cin >> u >> v;
if (isDirected) {
incMatrix[u][e] = -1; // from u
incMatrix[v][e] = 1; // to v
} else {
incMatrix[u][e] = 1;
incMatrix[v][e] = 1;
}
}
// Step 5: Display the incidence matrix
cout << "\nIncidence Matrix:\n";
for (int i = 0; i < V; i++) {
for (int j = 0; j < E; j++) {
cout << incMatrix[i][j] << " ";
}
cout << endl;
}
// Step 6: End
return 0;
}
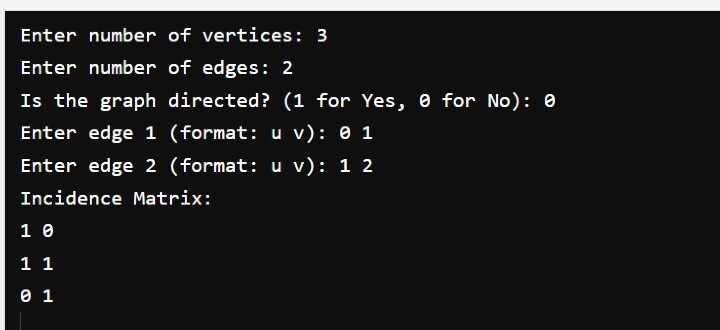
Sample Output
Here is a sample output of the above program.

Advertisements
