Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
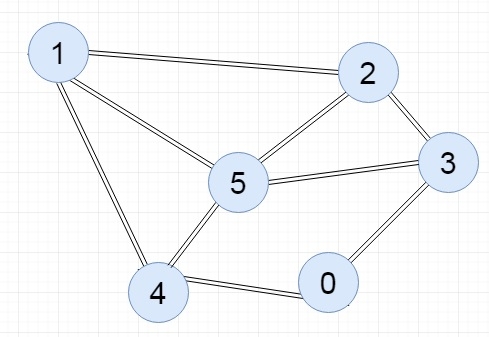
C++ Program to Represent Graph Using Linked List
The incidence matrix of a graph is another representation of a graph to store into the memory. This matrix is not a square matrix. The order of the incidence matrix is V x E. Where V is the number of vertices and E is the number of edges in the graph.
In each row of this matrix we are placing the vertices, and in each column the edges are placed. In this representation for an edge e {u, v}, it will be marked by 1 for the place u and v of column e.
The complexity of Adjacency Matrix representation
The incidence matrix representation takes O(V x E) amount of space while it is computed. For complete graph the number of edges will be V(V-1)/2. So incidence matrix takes larger space in memory.
Input:
Output:
Algorithm
add_edge(adj_list, u, v)
Input − The u and v of an edge {u,v}, and the adjacency list
Output − Adjacency List of the graph G
Begin Append v into the list at index u Append u into the list at index v End
Example Code
#include<iostream>
#include<list>
#include<iterator>
using namespace std;
void displayAdjList(list<int> adj_list[], int v) {
for(int i = 0; i<v; i++) {
cout << i << "--->";
list<int> :: iterator it;
for(it = adj_list[i].begin(); it != adj_list[i].end(); ++it) {
cout << *it << " ";
}
cout << endl;
}
}
void add_edge(list<int> adj_list[], int u, int v) { //add v into the list u, and u into list v
adj_list[u].push_back(v);
adj_list[v].push_back(u);
}
main(int argc, char* argv[]) {
int v = 6; //there are 6 vertices in the graph
//create an array of lists whose size is 6
list<int> adj_list[v];
add_edge(adj_list, 0, 4);
add_edge(adj_list, 0, 3);
add_edge(adj_list, 1, 2);
add_edge(adj_list, 1, 4);
add_edge(adj_list, 1, 5);
add_edge(adj_list, 2, 3);
add_edge(adj_list, 2, 5);
add_edge(adj_list, 5, 3);
add_edge(adj_list, 5, 4);
displayAdjList(adj_list, v);
}Output
0--->4 3 1--->2 4 5 2--->1 3 5 3--->0 2 5 4--->0 1 5 5--->1 2 3 4
1K+ Views
