
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Implement AVL Tree
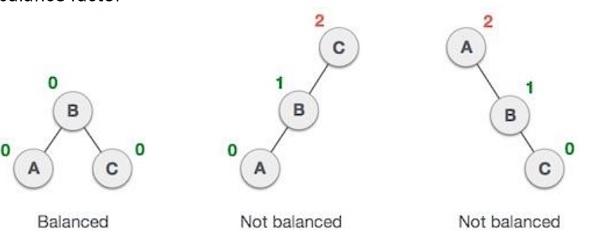
In this article, we will demonstrate how to implement an AVL tree. An AVL tree is a self-balancing binary search tree in which the height difference between the left and right subtrees (balance factor) of any node cannot exceed one.
AVL TREE
Following are the points of an AVL tree ?
- Tree rotation is a way to change the structure of an AVL tree without changing the order of the elements. It helps keep the tree balanced by moving one node up and one node down.
- Tree rotations are mainly used to reduce the height of the tree, which improves the performance of operations like searching, inserting, and deleting.
- A rotation works by shifting the nodes either to the left or to the right. This depends on which child node will take the place of the current root during the rotation.
Function Descriptions
Following are the function description before implementing the AVL tree ?
- height(avl *) : It calculate the height of the given AVL tree.
- difference(avl *): It calculate the difference between height of sub trees of given tree
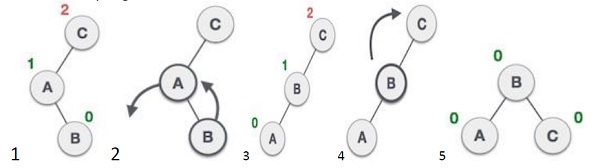
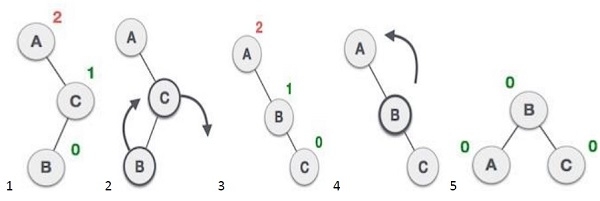
- avl *rr_rotat(avl *): A right-right rotation is a combination of right rotation followed by right rotation.
- avl *ll_rotat(avl *): A left-left rotation is a combination of left rotation followed by left rotation.
- avl *lr_rotat(avl*): A left-right rotation is a combination of left rotation followed by right rotation.
- avl *rl_rotat(avl *): It is a combination of right rotation followed by left rotation.
- avl * balance(avl *): It perform balance operation to the tree by getting balance factor
- avl * insert(avl*, int): It perform insert operation. Insert values in the tree using this function.
- show(avl*, int): It display the values of the tree.
- inorder(avl *): Traverses a tree in an in-order manner.
- preorder(avl *): Traverses a tree in a pre-order manner.
- postorder(avl*): Traverses a tree in a post-order manner
C++ Program to Implement AVL Tree
This is a simple C++ example to implement an AVL Tree, which includes tree rotations to keep the tree balanced ?
#include <iostream>
using namespace std;
// Structure for AVL tree node
struct avl {
int d;
struct avl * l;
struct avl * r;
};
// Global root node
avl * r = NULL;
// AVL Tree class
class avl_tree {
public: int height(avl * );
int difference(avl * );
avl * rr_rotat(avl * );
avl * ll_rotat(avl * );
avl * lr_rotat(avl * );
avl * rl_rotat(avl * );
avl * balance(avl * );
avl * insert(avl * , int);
void show(avl * , int);
void inorder(avl * );
void preorder(avl * );
void postorder(avl * );
};
// Height of node
int avl_tree::height(avl * t) {
if (!t) return 0;
return max(height(t -> l), height(t -> r)) + 1;
}
// Difference in height (balance factor)
int avl_tree::difference(avl * t) {
return t ? height(t -> l) - height(t -> r) : 0;
}
// Right-Right rotation
avl * avl_tree::rr_rotat(avl * parent) {
avl * t = parent -> r;
parent -> r = t -> l;
t -> l = parent;
return t;
}
// Left-Left rotation
avl * avl_tree::ll_rotat(avl * parent) {
avl * t = parent -> l;
parent -> l = t -> r;
t -> r = parent;
return t;
}
// Left-Right rotation
avl * avl_tree::lr_rotat(avl * parent) {
parent -> l = rr_rotat(parent -> l);
return ll_rotat(parent);
}
// Right-Left rotation
avl * avl_tree::rl_rotat(avl * parent) {
parent -> r = ll_rotat(parent -> r);
return rr_rotat(parent);
}
// Balance the AVL tree
avl * avl_tree::balance(avl * t) {
int bal_factor = difference(t);
if (bal_factor > 1) {
if (difference(t -> l) > 0)
t = ll_rotat(t);
else
t = lr_rotat(t);
} else if (bal_factor < -1) {
if (difference(t -> r) > 0)
t = rl_rotat(t);
else
t = rr_rotat(t);
}
return t;
}
// Insert a node
avl * avl_tree::insert(avl * root, int val) {
if (!root) {
root = new avl {
val,
NULL,
NULL
};
return root;
} else if (val < root -> d) {
root -> l = insert(root -> l, val);
} else {
root -> r = insert(root -> r, val);
}
return balance(root);
}
// Display tree structure
void avl_tree::show(avl * p, int l) {
if (p != NULL) {
show(p -> r, l + 1);
for (int i = 0; i < l; i++) cout << " ";
cout << p -> d << endl;
show(p -> l, l + 1);
}
}
// Inorder traversal
void avl_tree::inorder(avl * t) {
if (t) {
inorder(t -> l);
cout << t -> d << " ";
inorder(t -> r);
}
}
// Preorder traversal
void avl_tree::preorder(avl * t) {
if (t) {
cout << t -> d << " ";
preorder(t -> l);
preorder(t -> r);
}
}
// Postorder traversal
void avl_tree::postorder(avl * t) {
if (t) {
postorder(t -> l);
postorder(t -> r);
cout << t -> d << " ";
}
}
int main() {
avl_tree tree;
int values[] = { 30, 20, 40, 10, 25, 35, 50 };
int n = sizeof(values) / sizeof(values[0]);
for (int i = 0; i < n; ++i) {
r = tree.insert(r, values[i]);
}
// Display tree
cout << "Balanced AVL Tree Structure:\n";
tree.show(r, 1);
// Traversals
cout << "\nInorder Traversal: ";
tree.inorder(r);
cout << "\nPreorder Traversal: ";
tree.preorder(r);
cout << "\nPostorder Traversal: ";
tree.postorder(r);
cout << endl;
return 0;
}
Output
Balanced AVL Tree Structure:
50
40
35
30
25
20
10
Inorder Traversal: 10 20 25 30 35 40 50
Preorder Traversal: 30 20 10 25 40 35 50
Postorder Traversal: 10 25 20 35 50 40 30
Advertisements
